白酒是中国的一种古老蒸馏酒,也是中国的国酒,在中华传统文化中占有独特的地位[1]。传统的白酒生产方法已有数千年的历史,主要依靠个人的操作技能和经验。近年来,现代生物技术、自动化和电子信息技术的一些发展被应用到白酒生产中,以改进传统的加工方法。因此,在白酒生产中,大中型企业普遍采用半机械化生产工艺,以减轻劳动强度,改善白酒的品质和风味,减少人工劳动[2-3]。然而,这种生产方式仍然面临着缺乏可控性和规范性的问题。一些企业试图使用全机械化加工来生产白酒,但这影响了白酒的质量和风味。目前,白酒加工技术的发展正朝着全机械化、自动化、智能化的方向发展,同时也要保证白酒的质量和风味[4],而白酒双边固态酒精发酵过程的动力学建模是实现白酒加工技术自动化的核心与关键。
白酒的生产过程有别于其他蒸馏酒。在白酒的生产过程中,淀粉转化为糖与糖转化为酒精同时发生[5]。而在其他蒸馏酒的生产中,如威士忌和伏特加,上述两种反应是逐步发生的[6]。或者只有糖转化为酒精过程,例如朗姆酒[7]。除此之外,白酒的生产过程还是一种典型的固态发酵过程,中国几乎所有著名的优质白酒品牌都是用固态发酵生产的,这也是白酒与世界范围内的其他蒸馏酒最大的区别[5]。固态发酵体系中反应和热传递不均匀,并且白酒固态发酵传统的发酵容器通常设置在地下,很难监测它们的反应参数[5]。以上都使得白酒双边固态酒精发酵的动力学建模充满挑战性。
在国内外目前还没有研究涉及白酒固态双边发酵动力学建模,仅有一些淀粉液态同步糖化发酵或者纤维素固态发酵模型作为参考,且大多数研究采用的模型为非机理模型[8-10]。机理模型是根据对象、生产过程的内部机制或者物质流的传递机理建立起来的精确数学模型,参数易于调整并具有非常明确的实际意义,所得到的模型有很强的适应性,但往往需要大量的参数[11]。非机理模型是一种通过移动互联网或者其他的相关软件为手段采集海量的数据,将数据进行组织形成信息,之后对相关的信息进行整合和提炼,在数据的基础上经过训练和拟合,形成自动化的决策模型,这种模型往往适应性较弱,且参数没有实际意义,但是对于单个问题往往有很好的建模效果[11]。
1stOpt(First Optimization)平台中通用全局优化算法(universal global optimization,UGO)克服了当今世界上在优化计算领域中使用迭代法必须给出合适初始值的难题,即用户勿需猜测给出待求参数的初始值,由1stOpt随机给出,通过其独特的全局优化算法,最终找出最优解;遗传算法(genetic algorithm,GA)是计算数学中用于解决最优化的搜索算法,是进化算法的一种[12-13]。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的,这些现象包括遗传、突变、自然选择以及杂交等。
本研究利用实验室模拟白酒双边固态酒精发酵,基于实验室模拟发酵数据,创新性引入酶动力学方程,同时使用机理模型和非机理模型,建立白酒双边固态酒精发酵的动力学模型,描述酵母生长、葡萄糖形成、产物乙醇形成和底物糖分消耗的变化过程,并采用1stOpt的两种不同算法对模型参数进行辨识和拟合,以期为白酒双边固态酒精发酵过程的控制和优化提供一定的指导意义。
1 材料与方法
1.1 材料与试剂
发酵原料(高粱、麸皮、稻壳):江苏无锡玉祁酒业有限公司;盐酸、氢氧化钠、葡萄糖、蔗糖(均为分析纯):国药集团化学有限公司;醋酸-醋酸钠缓冲液(pH=4.5):福州飞净生物科技有限公司;氨苄青霉素钠(分析纯):西格玛奥德里奇(上海)贸易有限公司;葡萄糖淀粉酶(酶活力260000U/mL):夏盛(北京)生物科技开发有限公司;酿酒高活性干酵母(白酒王):安琪酵母股份有限公司。
1.2 仪器与设备
SPX-250B-Z生化培养箱:上海博讯实业有限公司;CT88A灭菌锅:上海伯能仪器有限公司;AL204分析天平:梅特勒-托利多国际贸易(上海)有限公司;SW-CJ-2FD超净工作台:苏净安泰空气技术有限公司;ST2100F酸度计:奥豪斯仪器(上海)有限公司;MQD-B3R振荡培养箱:上海旻泉仪器有限公司。
1.3 方法
1.3.1 白酒双边固态酒精发酵工艺流程及操作要点[14]
高粱→粉碎→润粮→加稻壳→蒸煮→加酶、加酵母→发酵
操作要点:称取600 g粉碎后的高粱,加入60 ℃热水540 mL润粮3 h,润粮完毕后加入60 g稻壳并混合均匀,放入蒸锅蒸煮30 min。取1 000 g蒸煮后高粱,摊凉冷却至60 ℃,加入稀释过的葡萄糖淀粉酶稀释液(酶活806 U/mL)溶液100 mL和活化好的干酵母(0.02 g/mL)100 mL,混合均匀。取140 g混合物加入组培瓶中30 ℃静置发酵,分别在发酵0 h、1 h、3 h、5 h、7 h、10 h、24 h、48 h、72 h、96 h、120 h、144 h、168 h时取样进行检测分析。
1.3.2 分析检测方法
葡萄糖含量的测定[15]:称取10 g固态发酵料于锥形瓶中,加入去离子水100 mL,30 ℃、200 r/min摇床振荡15 min,滤纸过滤,取浸出液,采用斐林试剂法测定浸出液中的葡萄糖含量。
淀粉含量的测定:称取5 g固态发酵料于锥形瓶中,加入20%盐酸100 mL,接入回流冷凝管,沸水浴加热30 min,迅速冷却后调节pH值为6.0,滤纸过滤,并将收集的滤液定容至500 mL,采用斐林试剂法测定浸出液的总糖含量,并计算得到淀粉含量,其计算公式如下[16]:
淀粉含量=(总糖-葡萄糖)/1.111
酵母含量的测定[15]:称取10 g固态发酵料于锥形瓶中,加入生理盐水100 mL,30 ℃、200 r/min振荡30 min,采用稀释涂布法计数。
乙醇含量的测定[15]:称取40 g固态发酵料于蒸馏烧瓶中,加入去离子水200 mL,直接蒸馏法蒸馏,准确量取70 mL馏出液,采用酒精计快速测定,并测定温度,经换算得固态发酵料的乙醇含量。
1.3.3 发酵动力学模型的构建[17-19]
(1)酵母(X)生长动力学模型
根据酵母生长可表示为酵母生长量与死亡量的差值,得出酵母生长动力学模型为:
式中:μ为酵母的比生长速率,h-1;X为酵母含量,g/10 g;Kd为细胞凋亡常数,h-1。
其中,
式中:μ为酵母的比生长速率,h-1;E为乙醇含量,g/10 g;Kxx为产物抑制常数,g/10 g。
(2)乙醇(E)生产动力学模型
根据乙醇由酵母生产,得出乙醇生产动力学模型为:
式中:q为乙醇的生产速率,h-1。
其中,
式中:qm为最大生产速率,h-1;Ksp为饱和生成常数,g/10 g;Kex为产物抑制常数,g/10 g。
(3)淀粉(S)水解动力学模型
根据淀粉水解可表示为淀粉的消耗量,得到淀粉水解动力学模型为:
式中:RS为淀粉的消耗速率,h-1;S为淀粉含量,g/10 g。
其中,
式中:Kh为速率常数,g/(U·h);Km为米氏常数,g/10 g。
(4)葡萄糖(G)转化动力学模型[20]
根据葡萄糖转化可表示为葡萄糖转化为乙醇和酵母维持生长的葡萄糖消耗[21-22],得到葡萄转化动力学模型为:
式中:系数1.111表示1 g淀粉完全水解时葡萄糖的理论产量1.111 g[16];YX/G为酵母生长的产率系数;YE/G为乙醇的产率系数;ms代表细胞维持系数[23],h-1。
(5)酶动力学模型
根据酶浓度的变化速率用酶活性增长速率、酵母生长时的酶消耗量和酶降解速率来表示,得出酶动力学模型为:
式中:Enz为酶的浓度,U/10 g;REnz 为酶浓度的变化速率,U/(10 g·h);β为酶的降解速率,h-1。
其中,
式中:KEnz 为酶的抑制常数,g/10 g;Enzm为酶的最大浓度,U/10 g。
1.3.4 参数辨识
由1.3.3可知,总体的模型由5个微分方程组成,共含有5个相关变量(X、E、S、G、Enz)和15个模型参数(Kh、Km、YX/G、YE/G、ms、μm、Ks、Kxx、Kd、qm、Ksp、Kex、Enzm、KEnz、β)[24]。采用1stOpt的通用全局优化算法和遗传算法[19]进行参数辨识及优化,寻优过程基于最小二乘法,目标函数可表示为:
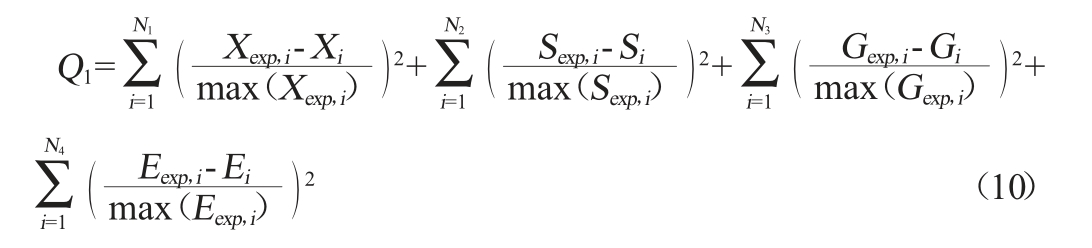
式中:N1、N2、N3和N4是用于参数辨识的可用实验数据的数目,Xexp、Sexp、Gexp和Eexp分别是酵母量、淀粉、葡萄糖和乙醇的已知实验数据,Xi、Si、Gi和Ei分别是酵母量、淀粉、葡萄糖和乙醇的预测值。
辨识模型参数的问题可以表示为求解目标函数(10)的最小值(min Q1):采用龙格-库塔-费尔博格法(Runge-Kutta-Fehlberg Method)对微分方程组求解[25]。
2 结果与分析
2.1 白酒双边固态酒精发酵过程分析
白酒双边固态酒精发酵过程中酵母、淀粉、葡萄糖和乙醇含量随时间变化的代谢曲线见图1。由图1可知,经过1 h的延迟期,酵母生长进入对数生长期,并在10 h左右,进入生长稳定期,之后进入衰落期;葡萄糖含量在5 h左右到达最大值后开始下降,并在96 h后停止减少,开始增加;说明随着乙醇含量的升高,导致酵母含量大量下降,酵母所消耗的葡萄糖开始少于酶解底物产生的葡萄糖。整个发酵周期乙醇含量逐渐增加,在96 h后趋于稳定,淀粉含量持续下降,在96 h后几乎不再减少,因此,可以将发酵周期控制在100 h之内。
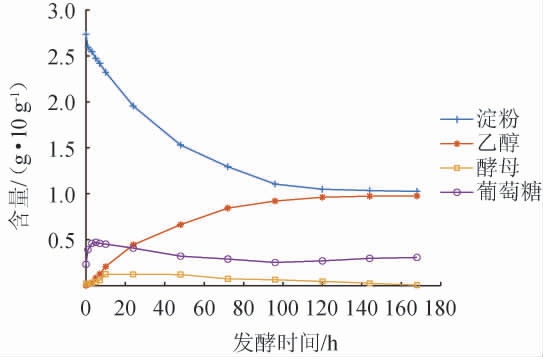
图1 白酒双边固态酒精发酵过程中淀粉、乙醇、葡萄糖及酵母含量的变化
Fig.1 Changes of the concentration of starch,ethanol,glucose and yeast during bilateral solid-state alcoholic fermentation of Baijiu
2.2 数据拟合和参数辨识
2.2.1 基于遗传算法酶动力学模型对拟合结果的影响
实验只得到了4个状态变量(X、E、S、G)的值,但上述提到了酶动力学模型。酶的状态变量表示在双边固态发酵过程中有效酶的集合,其主要是作用于淀粉的水解,所以模型中酶浓度变化的速率表示为淀粉含量的函数。而淀粉利用动力学与酶浓度密切相关,因此从计算的角度来看,如果淀粉含量预测的很好,则表明酶动力学模型辨识的参数也是合理的[26]。使用1stOpt,选择遗传算法(GA)对酶动力学模型引入前后的四个模型的预测值与实验值进行拟合,结果见图2。
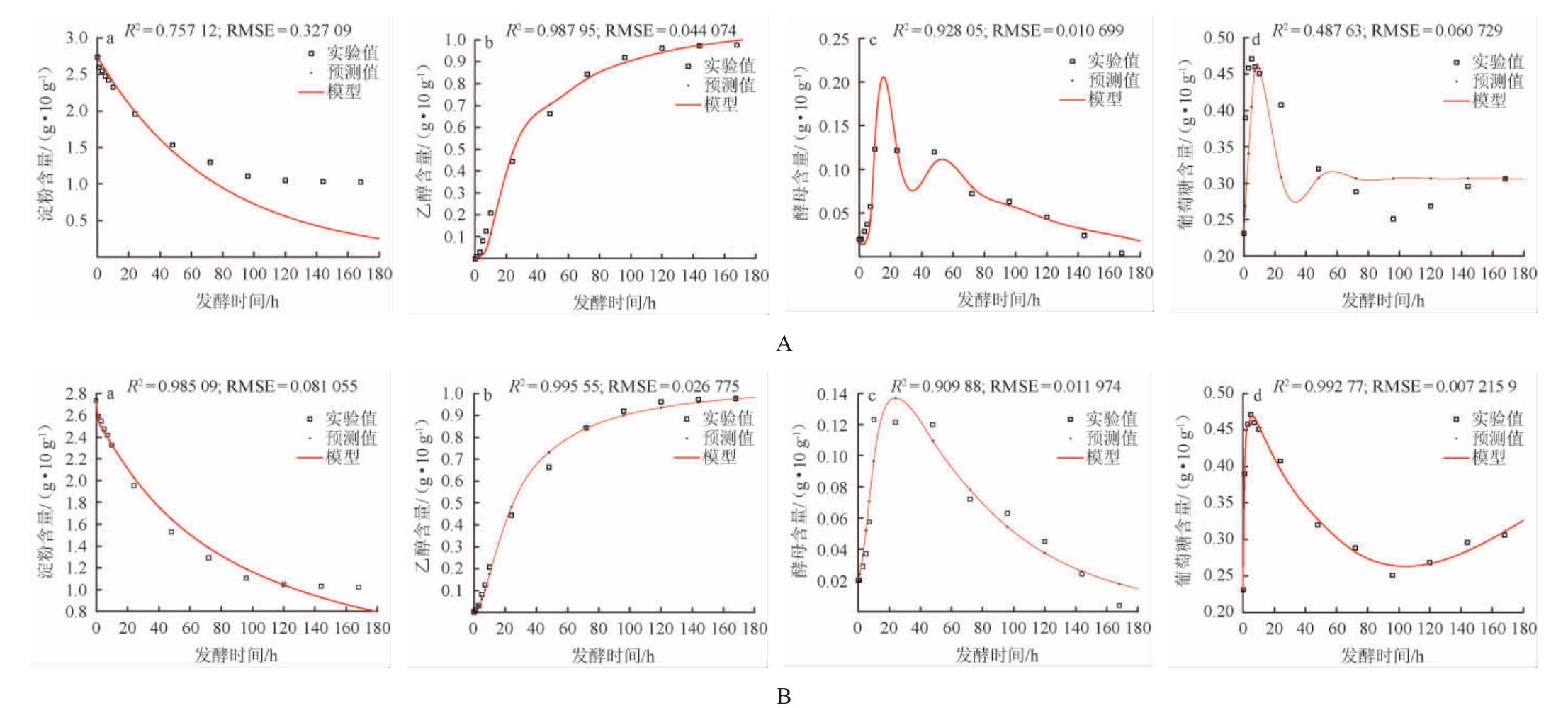
图2 引入酶动力学模型前(A)后(B)各模型预测值与实验值比较(遗传算法)
Fig.2 Comparison of predicted and experimental values of each model before (A) and after (B) the introduction of enzyme kinetics model (GA)
由图2可知,引入酶动力学模型前,拟合优度R2为0.828,引入酶动力学模型后,拟合优度R2提高至0.969,且淀粉(S)模型拟合优度R2达到0.985,证明酶动力学模型中的参数辨识结果是合理的。
2.2.2 通用全局算法对拟合结果的影响
采用通用全局算法(UGO)对酶动力学模型引入后4个模型的预测值及实验值进行拟合,结果见图3。
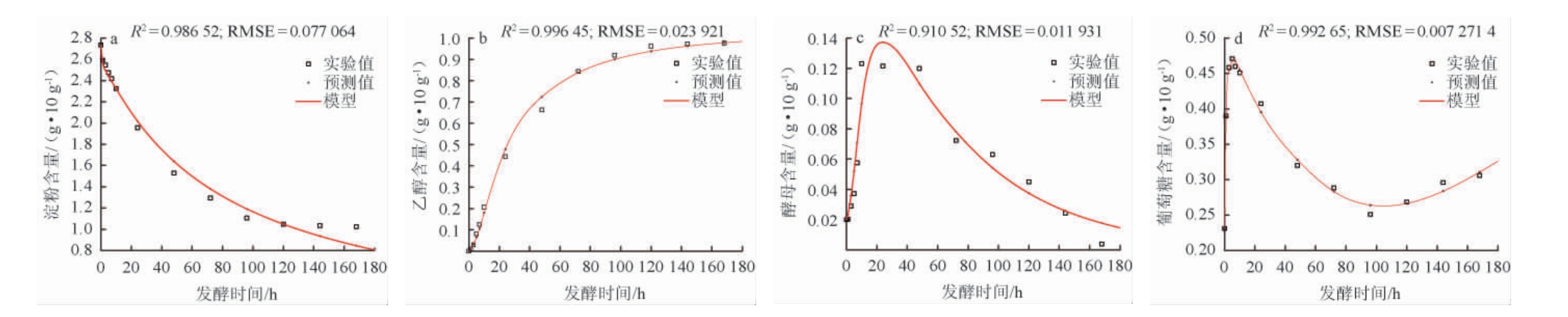
图3 引入酶动力学模型后各模型预测值与实验值比较(通用全局算法)
Fig.3 Comparison of predicted and experimental values of each model after the introduction of enzyme kinetics model (UGO)
结合图2和图3可知,使用UGO算法和GA算法的拟合结果从图形上来看没有明显差异,UGO拟合效果略微优于GA。模型拟合结果中,实验数据淀粉含量在120~180 h变化较小,但是模型中的淀粉含量在这一时期一直呈下降趋势,直到180 h时完全消耗底物;实验数据中酵母含量在10~60 h处于稳定期,变化很小,而模型的曲线则没有很好的体现出来,说明之后的模型优化和使用值得注意和改进。除此以外,模型能够很好的拟合实验数据。
结合图2和图3亦可知,UGO中除了葡萄糖转化模型的拟合结果评估(R2=0.992 65)略微小于GA(R2=0.992 77)外,其他三个模型拟合结果的拟合优度都要优于GA,拟合结果更好。UGO共迭代129次,花费时间约2.5 h,而GA共迭代1 000次仅花费了321 s,GA在运算效率上占据明显优势。
2.2.3 模型参数辨识结果
UGO和GA得到的模型参数辨识结果见表1。
表1 模型参数辨识结果
Table 1 Identification results of model parameters
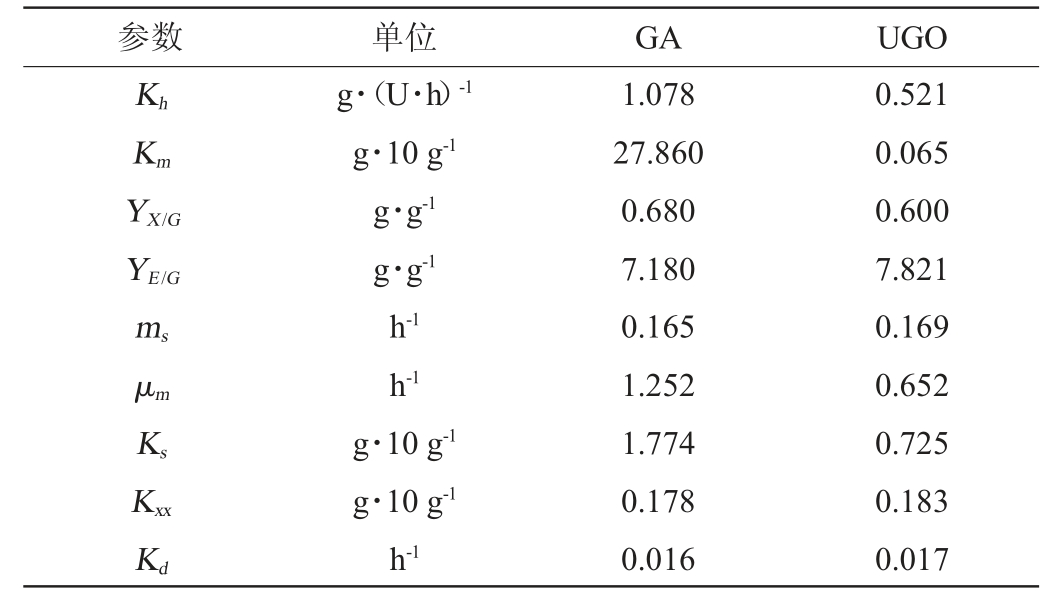
续表
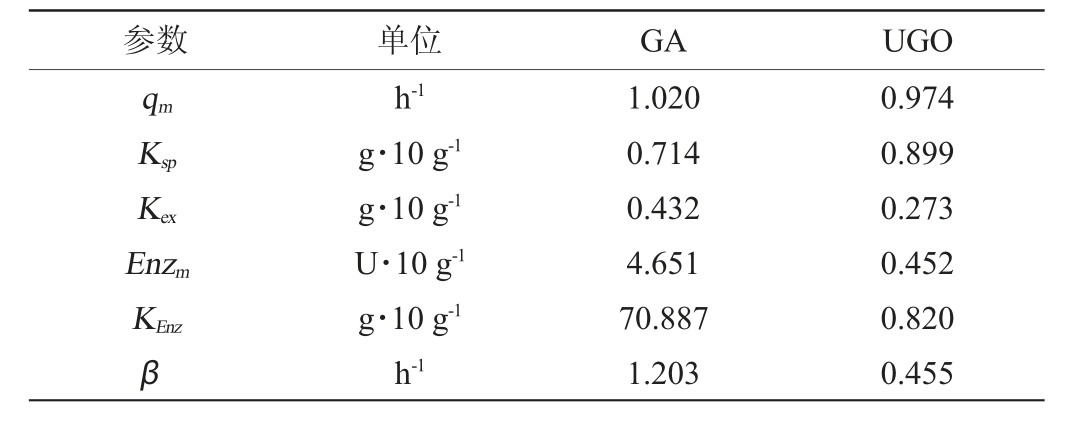
由表1可知,两种算法在乙醇动力学模型和葡萄糖转化模型上得到的参数差异较小,而在淀粉水解模型、酵母生长模型和酶动力学模型上有一定差异。从实际意义上来看,GA得到的参数Km为27.86 g/10 g,KEnz为70.89 g/10 g,而实际上淀粉含量(S)最高只有2.8 g/10 g左右,明显不具有实际意义,而UGO得到的参数更加合理。可能是因为GA在全局优化能力上明显弱于UGO,遇到复杂问题时容易陷入局部最小值[27]。
3 结论
本研究基于实验室发酵实验数据,以白酒酒精固态发酵过程为建模基础,建立了白酒双边固态酒精发酵的动力学模型,描述了酵母生长、葡萄糖形成、产物乙醇形成和底物糖分消耗变化过程,并对模型参数进行辨识和非线性拟合。创新性地引入了酶动力学模型,在没有获得酶浓度数据的情况下,使得拟合结果得到了更大的提升。淀粉含量的准确预测,表明了酶动力学模型辨识参数的合理性。UGO的拟合结果略优于GA,GA的算法效率高于UGO。但是GA在面对复杂问题,或者寻优函数不合适时,往往会过早收敛。因此,从拟合参数的实际意义来看,UGO的结果更加具有实际意义。采用UGO得到淀粉水解、葡萄糖转化、酵母生长、乙醇生产4条拟合曲线的拟合优度R2分别达到0.986 52、0.992 65、0.910 52和0.996 45,除了酵母生长模型(0.910 52)以外,其他模型的拟合优度R2都远大于0.95,说明模型在统计学意义上是成功的,对白酒双边固态发酵过程的优化和控制具有很大帮助,并且对白酒生产工艺的自动化发展具有重要意义。但是,白酒实际发酵过程中传质与传热的不均匀,温度因素尚未被考虑在本研究的模型中,这也是下一步研究发展的方向。而且白酒的发酵过程除了酵母参与的酒精发酵,还有很多霉菌和细菌的参与,混菌发酵模型也是未来探讨的一大难点。
[1]MCGOVERN P E,ZHANG J,TANG J,et al.Fermented beverages of preand proto-historic China[J]. Proc Natl Acad Sci USA,2004,101(51):17593-17598.
[2]李玉彤,齐士朋,邱利华.白酒机械化酿造研究进展与探讨[J].酿酒科技,2016(10):82-84.
[3]谢齐鸣.白酒酿造机械化新工艺设备系统的实践[J].酿酒,2012,39(2):43-49.
[4]YE H,WANG J,SHI J,et al.Automatic and intelligent technologies of solid-state fermentation process of Baijiu production:Applications,chal-lenges,and prospects[J].Foods,2021,10(3):680.
[5]LIU H,SUN B.Effect of fermentation processing on the flavor of Baijiu[J].J Agr Food Chem,2018,66(22):5425-5432.
[6]THIBAUD F,PETERSON A,URRUTY L,et al.Sensorial impact and distribution of 3-methyl-2,4-nonanedione in Cognacs and spirits[J]. J Agr Food Chem,2021,69(15):4509-4517.
[7]MANGWANDA T,JOHNSON J B,MANI J S,et al.Processes,challenges and optimisation of rum production from molasses-a contemporary review[J].Fermentation,2021,7(1):21.
[8]宗原.基于黄酒发酵过程的建模与优化研究[D].无锡:江南大学,2021.
[9]刘登峰,熊伟丽,徐玲.黄酒双边发酵过程的建模[J].系统仿真学报,2014,26(3):626-630,674.
[10]王二强,耿欣,李十中.甜高粱秆分批固态发酵制乙醇动力学研究[J].食品与发酵工业,2009,35(10):1-4.
[11]周健民,沈仁芳.土壤学大辞典[M].北京:科学出版社,2013:206-209.
[12]孙立珍,赵乐乐.基于MATLAB和1stOpt的非线性曲线拟合比较[J].现代计算机,2020(31):28-30,37.
[13]边霞,米良.遗传算法理论及其应用研究进展[J].计算机应用研究,2010,27(7):2425-2429,2434.
[14]高银涛,何璇.白酒固态双边发酵糖化机理及其对发酵过程的影响[J].食品与发酵工业,2021,47(13):92-97.
[15]沈怡方.白酒生产技术全书[M].北京:中国轻工业出版社,1998:497-502.
[16]KROUMOV A D,AN MÓDENES,TAIT M.Development of new unstructured model for simultaneous saccharification and fermentation of starch to ethanol by recombinant strain[J].Biochem Eng J,2006,28(3):243-255.
[17]OCHOA S,YOO A,JENS-UWE REPKE,et al.Modeling and parameter identification of the simultaneous saccharification-fermentation process for ethanol production[J].Biotechnol Progr,2010,23(6):1454-1462.
[18]SINGH S,CHAKRAVARTY I,PANDEY K D,et al.Development of a process model for simultaneous saccharification and fermentation(SSF)of algal starch to third-generation bioethanol[J]. Biofuels,2018,11(7):847-855.
[19]雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014:139-150.
[20]EKLUND R,ZACCHI G.Simultaneous saccharification and fermentation of steam-pretreated willow[J].Enzyme Microb Tech,1995,17(3):255-259.
[21]HARI KRISHNA S,CHOWDARY G.Optimization of simultaneous saccharification and fermentation for the production of ethanol from lignocellulosic biomass[J].Agr Food Chem,2000,48:1971-1976.
[22]LIU D,XU L,XIONG W,et al.Fermentation process modeling with Levenberg-Marquardt algorithm and Runge-Kutta method on ethanol production by Saccharomyces cerevisiae[J]. Math Probl Eng,2014,2014:1-10.
[23]D JIMÉNEZ-ISLAS,J PÁEZ-LERMA,SOTO-CRUZ N O,et al.Modelling of ethanol production from red beet juice by Saccharomyces cerevisiae under thermal and acid stress conditions[J].Food Technol Biotech,2014,52(1):93-100.
[24]ALTNTA M M,BETÜL KRDAR,LGEN K.Cybernetic modelling of growth and ethanol production in a recombinant Saccharomyces cerevisiae strain secreting a bifunctional fusion protein[J].Process Biochem,2002,37(12):1439-1445.
[25]SIMOS T E.A Runge-Kutta Fehlberg method with phase-lag of order infinity for initial-value problems with oscillating solution[J]. Comput Math Appl,1993,25(6):95-101.
[26]JANG M F,CHOU Y S.Modeling and optimization of bioethanol production via a simultaneous saccharification and fermentation process using starch[J].J Chem Technol Biot,2013,88(6):1164-1174.
[27]王铁方.计算机基因学:基于家族基因的网格信任模型[M].北京:国家知识产权局知识产权出版社,2016:98-103.