Research on grade classification of strong-flavor Baijiu base liquor based on unbalanced data sets
中国白酒是一种以糯米、高粱、玉米等谷物为主要原料的酒精饮料[1],其香型众多,浓香型白酒以其香气浓郁、口感绵甜醇厚而著称,在中国白酒市场占据重要地位,其市场份额曾一度达到70%以上,是中国白酒生产和消费的主流[2]。由于原料的复杂性和工艺的独特性,白酒基酒中的成分异常丰富多样,仅占1%~2%左右的微量成分赋予了白酒独特的风味和香气,决定着白酒的品质差异。传统的基酒品质分析主要依赖于专业品评员的感官体验,但由于其易受到环境条件和个体主观性的影响,评估结果缺乏客观性和一致性,无法实现基酒品质判别的准确性和客观性[3]。
近年来,仪器分析作为一种快速、准确的检测手段,逐渐广泛应用于白酒等食品领域,如气质联用(gas chromatography-mass spectrometry,GC-MS)[4]、近红外光谱(near infrared spectrometry,NIR)[5]、电子鼻(electronic nose,E-nose)[6]、核磁共振(nuclear magnetic resonance,NMR)[7]等技术。其中GC-MS是一种结合色谱高分辨能力和质谱高灵敏度的先进分析技术,在白酒分类识别中获得了较好的性能。钱宇等[8]利用GC-MS技术检测浓香型白酒成分,并结合主成分分析(principal component analysis,PCA)方法实现了对不同品牌白酒的分类。陈明举等[9]利用GC-MS技术结合稀疏主成分(sparse principal component analysis,SPCA)和回归分析建立了浓香型白酒等级判别模型。朱开宪等[10]利用GC-MS技术结合化学计量学手段实现了对不同香型的白酒分类。
目前,在基于GC-MS技术的白酒分类识别研究中,大多数方法是在类别分布平衡的条件下实现的,然而在实际白酒市场上白酒品质参差不齐是一个普遍存在的现象[11],这通常会导致不同品质的白酒之间存在数量不均衡问题。而常用的分类方法往往难以充分学习到少数类的样本信息,导致难以达到理想的分类效果。因此,研究不平衡的浓香型白酒基酒分类可以帮助生产企业更好地生产不同品质的白酒并满足市场需求,对白酒产业的发展和升级具有意义。目前针对非均衡数据的处理方法可以分为两个方面:数据层面和算法层面。在数据层面主要采用欠采样和过采样这两种技术[12]。欠采样技术是通过减少多数类样本数量,使分类器更专注于少数类样本,常用方法是随机欠采样[13],欠采样技术的主要优点是所有训练数据都是真实的,然而它可能会忽略潜在的有效信息;过采样技术则是增加少数类样本来平衡数据分布,常用的有随机过采样和合成少数类过采样技术(synthetic minority over-sampling technique,SMOTE),随机过采样只是简单地复制少数类样本,容易出现过拟合问题[14],合成少数类过采样技术SMOTE[15]是一种强大的均衡数据集的方法,被广泛应用于各个领域[16]。算法层面的主要思想是结合实际数据分布,对现有的分类算法模型进行适当修改[17],目前使用较多的是集成学习算法,常见的集成学习方法有Bagging算法、Boosting算法和随机森林算法(random forest,RF)[18]等。王磊等[19]提出加权随机森林有效提高了不平衡数据集的整体分类性能,ZHOU Z H等[20]改进了随机森林算法,提出了深度森林算法(deep forest,DF),避免了随机森林复杂的调参过程,具有更好的识别率。然而,针对样本不平衡数据情况下的基酒分类识别问题还未有研究及报道。
本实验将研究在样本不平衡条件下对浓香型白酒基酒通过GC-MS检测技术获得的46种挥发性风味成分进行定性和定量分析,通过SMOTE对基酒数据进行扩充,增加数据集的平衡性,并通过稀疏主成分分析(SPCA)对GC-MS图谱数据进行特征降维,最后采用深度森林算法对白酒基酒数据进行分类识别,同时与RF算法、支持向量机算法(support vector machines,SVM)[21]对比分析,以期为数据不均衡条件下的浓香型白酒基酒分类识别提供理论依据和方法。
1.1.1 白酒样品
产自川南地区不同质量等级的浓香型白酒基酒样品,经过感官品评分为一级、二级、优级、特级共四个等级,每个等级包含的样本数量依次为73个、17个、42个、10个。
1.1.2 试剂
正构烷烃(C7~C40)(均为色谱纯):北京曼哈格生物科技有限公司;无水乙醇(纯度>99.5%):上海阿拉丁试剂有限公司;甲醇(纯度>99.9%):美国Sigma-Aldrich有限公司。
7890A-5975C气相色谱-质谱联用仪、HP-5ms毛细管柱(30 m×0.25 mm×0.25 μm):美国安捷伦科技有限公司。
1.3.1 挥发性风味成分GC-MS分析
GC条件:色谱柱为HP-5ms毛细管柱(30 m×0.25 mm×0.25 μm)。载气为高纯氦气(He),载气流速1mL/min;进样量1 μL,进样方式为分流进样,分流比为20∶1;进样口温度250 ℃;升温程序:初始温度40 ℃保持1 min,以10 ℃/min的升温速度升温到120 ℃(2 min),再以10 ℃/min升温到200 ℃(2 min),最后以10 ℃/min升温到250 ℃,保留时间为2 min。
MS条件:电子电离(electronic ionization,EI)源:电子能量70 eV;离子源温度230 ℃;接口温度280 ℃;采用全扫描模式;质量扫描范围29~500 m/z。
定性分析方法:采用与样品集完全相同的参数进行正构烷烃标准品(C7~C40)测定,计算保留指数(retention index,RI),与美国国家标准技术研究所(national institute of standards and technology,NIST)12谱库进行比对,保留匹配度>85%的化合物。
定量分析方法:采用峰面积归一化法。
1.3.2 SMOTE算法原理及分类模型评价指标
(1)SMOTE算法基本原理
类别分布不均衡是一种在分类器模型训练过程中常见的问题之一,SMOTE算法是一种常用的解决类别不平衡的数据处理技术,它是对随机过采样算法的一种改进,旨在克服随机过采样可能引发的过拟合问题,相比于随机过采样算法,SMOTE过采样具有更好的泛化能力,尤其在少数类别样本数量非常有限的情况下,可以有效提升模型的性能和稳定性,因此在处理样本不均衡问题时被广泛应用[22]。为了提升模型的分类效果并降低过拟合风险,本研究提出将SMOTE应用到不均衡的白酒样本中。SMOTE算法的基本思想对于每个少数类别样本xi,选取它的k个邻近样本xi,near,然后在这些样本之间进行插值,生成新的合成样本xnew。新样本合成公式如下:
xnew=xi+rand(0,1)×(xi,near-xi)
式中:rand(0,1)表示0~1之间的随机数。
(2)稀疏主成分分析基本原理
主成分分析(PCA)是一种无监督学习方法[23],它通过线性组合所有原始变量,生成一组新的特征向量,称为主成分,然而,由于这些主成分是原始变量的线性组合,其解释性通常较差。SPCA是PCA的一种扩展,相较于传统的PCA算法,SPCA在降维的过程中引入了稀疏性的概念,并在优化问题中使用lasso惩罚项,这使得优化问题变为一个稀疏化问题[24],即在降维过程中会生成稀疏的特征向量,突出主要成分,这可以更好的体现基酒中的微量成分与品质之间的关系。本研究将基于SPCA方法对基酒图谱数据进行稀疏主成分提取并建立白酒品质分析模型。SPCA的计算步骤如下:
①初始化A=V[1∶k],其中V是PCA算法得出的前k个主成分的载荷矩阵。
②对于给定的A=[α1,…,αk],添加L1正则项对回归系数进行惩罚获得稀疏的系数:
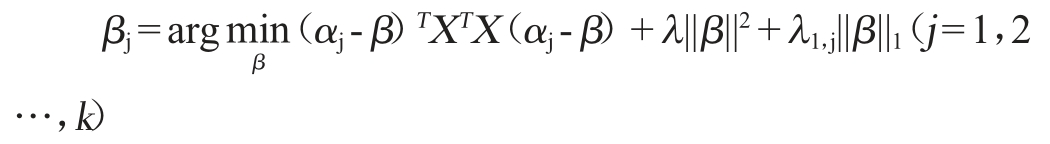
③对于给定的B=[β1,…,βk],计算的XTXB=UDVT的SVD,更新A=UVT。
重复步骤②和③直至收敛。
④标准化之后得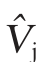 :
:
1.3.3 深度森林算法基本原理
集成学习算法通过将多个弱分类器组合成强分类器,可以降低模型的偏差和方差,提高模型的鲁棒性,常用来解决数据分类不平衡问题。深度森林算法是基于决策树的“集成中的集成”,结合了深度学习和随机森林的思想[20]。该模型具备优秀的特征表示学习能力以及较少的超参数量,十分适用于小规模数据分析,对不平衡数据集有较好的鲁棒性,一定程度上能克服传统机器学习的不足,因此本研究选用DF作为分类器。
深度森林主要包括级联森林和多粒度扫描两个部分。多粒度扫描结构利用多种大小的滑动窗口进行采样,以获得更多的特征子样本,从而达到多粒度扫描的效果。一个滑动窗口的多粒度扫描结构如下:
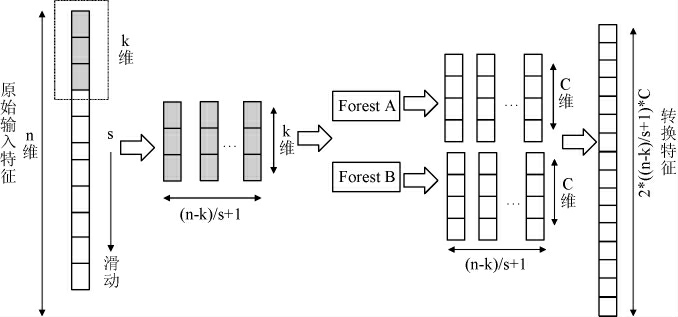
在多粒度扫描结构中,原始输入特征为n维,滑动窗口大小为k维,滑动步长为s(一般取1),则原始特征通过该滑动窗口得到(n-k)/s+1个k维特征子样本,然后这些子样本再经过森林A和森林B的训练,获得C维的概率向量,最后将所有森林产生的C维概率向量进行串联,计算得到最终的转换特征。
多粒度扫描是对级联森林的增强,级联森林将多粒度扫描最终输出的特征向量作为其输入向量,并送入后续模型结构进行有监督训练。它通过将多个森林组成一个级联结构,每一层都对数据进行进一步的筛选和处理。级联森林结构如下:
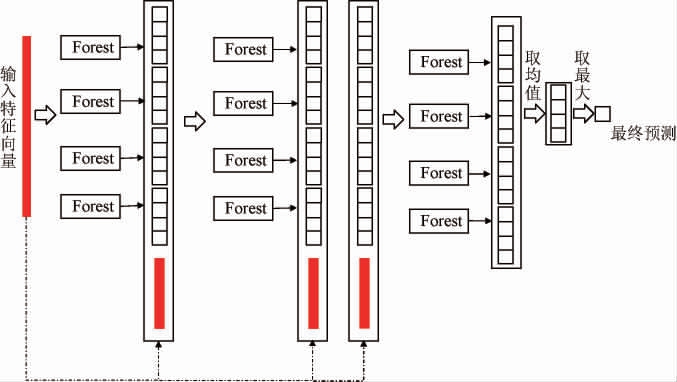
在级联森林结构中,第一层森林用于初步筛选样本,将大部分易分类的样本从数据集中剔除;然后,通过级联过程,将剩余的难分类样本传递给下一层森林进行更深入的分类。通过这种方式就能逐层筛选样本和加强分类器的方式提高整体分类性能,尤其适用于处理高度不平衡的数据集。在该级联森林中每层有4个随机森林,而每个森林都将生成一个4维向量,因此每层产生16维的特征向量,并将其作为下一层的输入。最后一层将所有森林输出的4维向量求平均并取最大值作为最终输出结果。多粒度扫描结构和级联森林结构相结合即为深度森林模型,深度森林总体结构如下:
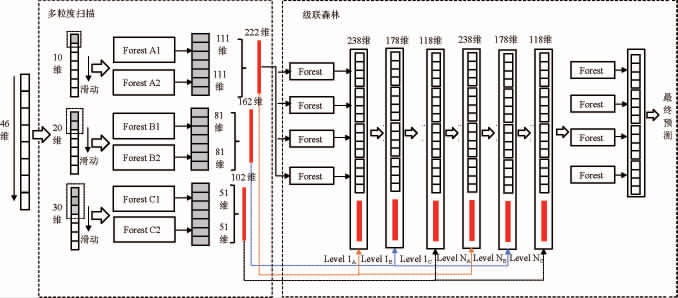
在深度森林总体结构中,首先将46维原始特征向量送入多粒度扫描结构,经过3个滑动窗口进行滑动扫描并导入到随机森林中转换为类向量进行拼接,然后将转换后的分类向量作为级联森林的输入特征,级联森林经过逐层训练直到模型性能不再提升,最后输出所有森林生成的各类概率分布求平均,选取最大值作为最终预测结果。
1.3.4 分类模型评价指标
在处理非均衡数据时,分类器往往会将少数类误分为多数类,使用准确率这一评价指标不能够准确评价非均衡数据的分类模型,因此本研究除了准确率(accuracy,Acc)指标外,另引入基于精确率(precision,Prec)和召回率(recall,Rec)的F1值以及几何平均(geometric mean,G-mean)值作为分类模型的评价指标,以二分类为例,混淆矩阵见表1。
表1 混淆矩阵
Table 1 Confusion matrix
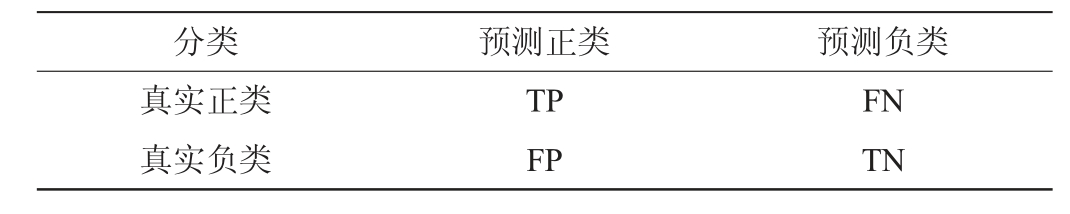
分类 预测正类 预测负类真实正类真实负类TP FP FN TN
其中,TP(true positive)表示正确识别的正类样本数量;TN(true negative)表示正确识别的负类样本数量;FN(false negative)表示误将正类预测为负类的样本数量;FP(false positive)表示误将负类预测为正类的样本数量。基于上述混淆矩阵,Acc、F1值、G-mean等评价指标计算公式如下:
Acc=(TP+TN)/(TP+TN+FP+FN)
F1=2×Prec×Rec/(Rec+Prec)
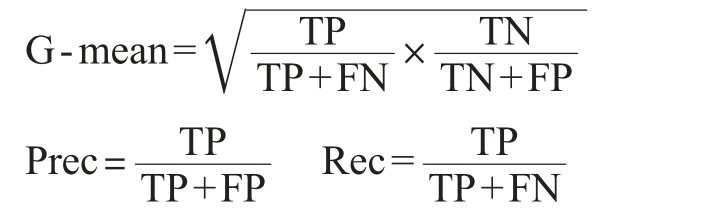
式中各指标取值范围均为0~1,准确率表示正确预测样本数量占总样本的比例,但在非平衡数据中无法保证少数类的识别效果;精确率表示所有正类中正确预测的比例;召回率衡量了模型是否能够捕获到所有正例,召回率越高表明某类样本被正确识别的数量越多;而F1值则是基于精确率和召回率的调和平均值,综合考虑了模型的预测准确性和召回能力[25];G-mean是真正例率和真负例率的几何平均值,真正例率衡量了模型正确分类为正类的样本比例,真负例率衡量了模型正确分类为负类的样本比例,因此G-mean能够更好地衡量分类器在多类别不平衡数据集上的整体性能,尤其对于少数类的分类效果有更好的反映。因此对于不均衡数据分类通常使用G-mean和F1值作为评价指标。
若是多分类问题,例如对于一个m分类(m>3),则要根据m×m的混淆矩阵计算每一个类别的召回率,精确率、F1值、G-mean和准确率然后取均值作为最终的结果。
本实验参照国标GB/T 10345—2022《白酒分析方法》标准对浓香型白酒基酒酒样进行感官评定。将浓香型白酒基酒酒样进行编号并送泸州某知名白酒公司进行感官品评。总分为100分,采用均值法记录各基酒酒样得分。其中95~100分之间为特级,90~95分之间为优级,80~90分之间为一级,70~80分之间为二级,70分以下为其他。
结果表明,一级基酒数量最多(73个),二级基酒数量为17个,优级基酒数量为42个,特级基酒数量最少(10个)。这是因为在经过蒸馏后得到的基酒会根据其质量特点和风味进行评定和等级划分,并分别入库,市场上最常见的就是一级和优级基酒。特级基酒指酒醅蒸馏过程中的中前段酒,这部分酒各种风味成分数量和比例特别协调,是基酒中质量最好的酒,但其比例非常少,主要用于调制高端产品;优级基酒通常是特级酒馏出后的部分,这部分的酒体非常干净,质量较好,可用于调制次高端产品;一级基酒通常是中段酒,酒体的主体香相对来说不是特别突出,其产量最高;二级基酒通常指后段酒,这部分的酒体一般主体香低,一般品质较差,常用于调制低档产品。
采用上述GC-MS实验方法,计算得到基酒样品中挥发性风味物质的相对含量,其中某一基酒样品挥发性风味物质的分析结果表2。
表2 代表基酒样品挥发性风味物质GC-MS分析结果
Table 2 Results of volatile flavor compounds contents in representative base liquor sample analysis by GC-MS

序号 化合物 相对含量/% 序号 化合物 相对含量/%1 2 3 4 5 6 7 8 9 1 0 11 12 13 14 15 16 17 18 19 20 21 22 23甲醇乙醛乳酸正丙醇乙酸乙酯2-丙醇异戊醛正丁醇2-戊酮异戊醇丙酸乙酯乙缩醛3-甲基丁醇2-甲基丁醇异丁酸乙酯正戊醇丁酸丁酸乙酯乳酸乙酯糠醛异戊酸乙酯丁缩醛乙基苯0.793 0.293 0.022 2.328 10.349 3.028 0.144 3.524 0.048 0.132 0.361 4.531 1.953 0.480 0.143 0.205 2.411 5.967 4.689 0.164 0.092 0.054 0.241 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46正己醇己酸异戊酯正戊酸对二甲苯戊酸乙酯戊缩醛异己酸乙酯己酸己酸乙酯己酸丙酯庚酸乙酯己酸丁酯辛酸乙酯苯乙酸乙酯己酸戊酯苯乙基苯丙酸乙酯己酸己酯癸酸乙酯十四酸乙酯十六酸乙酯十八酸乙酯己酸甲酯2.037 0.023 0.251 0.256 1.274 0.367 0.036 9.338 41.561 0.136 0.555 0.475 0.497 0.090 0.070 0.027 0.033 0.392 0.028 0.032 0.314 0.188 0.071
由表2可知,从浓香型白酒代表性基酒中共鉴定出46种挥发性风味物质,包含醛类6种,酯类23种,醇类9种,酸类4种,以及其他少量苯类和酮类物质。可以看出酯类物质在浓香型白酒基酒中含量相对较高,其中己酸乙酯含量最高。
采用SPCA算法对GC-MS技术检测的浓香型白酒代表性基酒中46种挥发性风味物质进行特征提取。稀疏主成分分析后前10个稀疏主成分的特征值、方差贡献率以及累计方差贡献率见表3。
表3 稀疏主成分分析主成分特征值与累计方差贡献率
Table 3 Eigenvalues of principal components and cumulative variance contribution rates of sparse principal components analysis
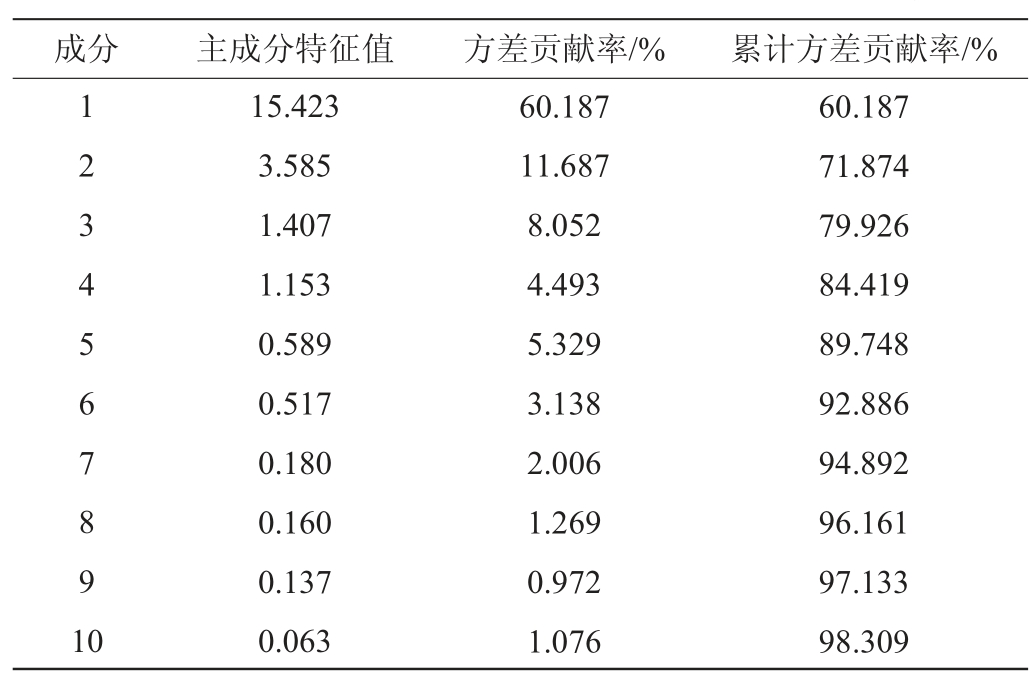
成分 主成分特征值 方差贡献率/% 累计方差贡献率/%1 2 3 4 5 6 7 8 9 1 0 15.423 3.585 1.407 1.153 0.589 0.517 0.180 0.160 0.137 0.063 60.187 11.687 8.052 4.493 5.329 3.138 2.006 1.269 0.972 1.076 60.187 71.874 79.926 84.419 89.748 92.886 94.892 96.161 97.133 98.309
由表3可知,前10个稀疏主成分的累计方差贡献率为98.309%,前6个稀疏主成分的累计方差贡献率为92.886%,说明选取前6个稀疏主成分基本能够反映原浓香型基酒挥发性风味物质的大部分信息。
为了更好的利用有限的样本数量,关注到每个类别的特征,本研究基酒数据集采用分层抽样的方式,按照4∶1的比例将数据集划分为训练集和测试集,进行模型训练和验证。为了更好地比较不均衡样本的分类性能,本研究首先使用SVM、Adaboost、RF算法对未扩充数据集进行实验,结果见表4。实验过程中,SPCA选取前6个稀疏主成分特征作为输入数据;SVM算法采用“一对多”策略,核函数采用径向基函数;Adaboost算法选择ZHU J等[26]提出的SAMME.R版本,使之适用于多分类问题;同时Adaboost、RF、DF和SVM算法均使用网格搜索的方式确定最优参数。模型验证采用1.3.4节提到的准确率、G-mean及F1值作为评价指标。
表4 不均衡样本下各算法分类结果
Table 4 Classification results of each algorithm under unbalanced samples
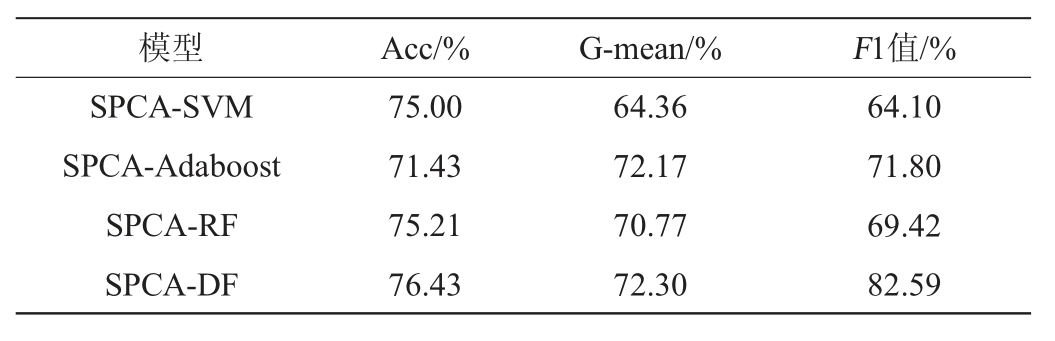
模型 Acc/% G-mean/% F1值/%SPCA-SVM SPCA-Adaboost SPCA-RF SPCA-DF 75.00 71.43 75.21 76.43 64.36 72.17 70.77 72.30 64.10 71.80 69.42 82.59
由表4可知,整体而言,这几种机器学习算法的准确率、G-mean和F1值都不是很高,这是因为它们在处理不均衡样本分类问题时,通常会使结果倾向于多数类样本,从而导致少数类样本分类结果降低,所以不适合直接用于不均衡样本。为此,通过前文的分析,使用SMOTE算法生成少数类样本以均衡数据集。原始样本数据中,一级基酒样品是73个,是所有样品中最多的,因此将其他3类基酒酒样进行SMOTE过采样后的样本规模全部设置为73个,最终获得292个均衡后的样本集。均衡后的分类结果分别见表5和图1。
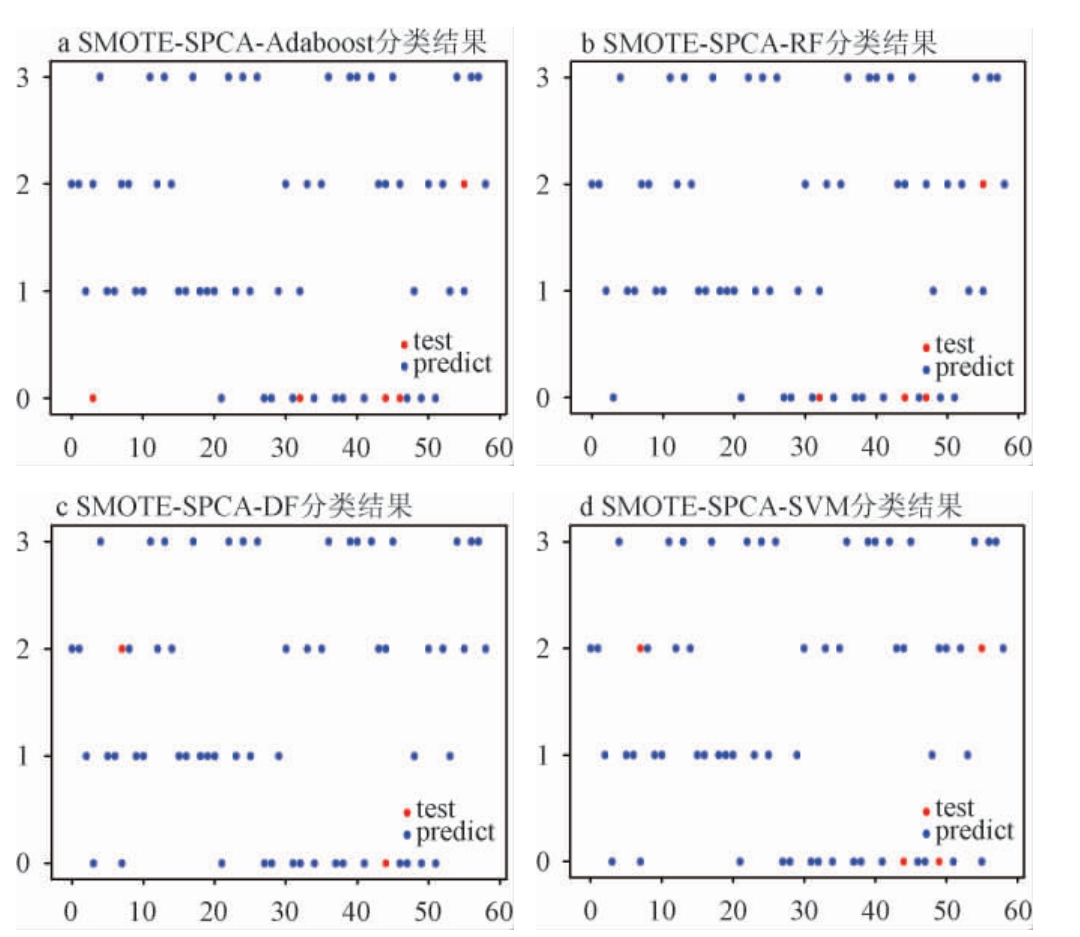
图1 基于稀疏主成分分析的浓香白酒基酒测试集分类结果
Fig.1 Test set classification results of strong-flavor Baijiu base liquor based on sparse principal components analysis
表5 均衡样本下各算法分类结果
Table 5 Classification results of each algorithm under balanced samples

模型 Acc/% G-mean/% F1值/%SMOTE-SPCA-Ada SMOTE-SPCA-RF SMOTE-SPCA-DF SMOTE-SPCA-SVM 91.53 93.36 96.61 93.22 91.46 93.27 96.00 93.10 91.23 93.18 96.59 93.00
由表5可知,在均衡样本后这几种模型的准确率均有明显提升,SPCA结合SVM、Adaboost、RF和DF算法的准确率、G-mean和F1值均能达到90%以上,其中DF算法的准确率、G-mean及F1值都最高,最终准确率达到96.61%。其结果表明在使用SMOTE算法扩充少数类样本后,能够使更多的少数类样本得到正确的区分,有助于提高分类器整体分类能力,在对比方法中,SMOTE-SPCA-DF方法表现最佳。
由图1可知,Adaboost、RF、DF和SVM算法在测试集的误检样本数分别为5个、4个、2个和4个。由此可见,SMOTE结合SPCA和DF的方法能够在实现数据降维的同时,有效提高白酒基酒分类准确率。
本研究基于GC-MS技术检测分析浓香型白酒基酒的挥发性风味物质的相对含量,研究在白酒基酒数据集类间分布不均衡的情况下,提出采用SMOTE算法进行少数类样本合成,得到均衡的数据集,并使用SPCA进行数据特征降维,去除冗余信息,最后使用深度森林集成算法分类器建立浓香型白酒基酒的等级分类识别模型。研究结果表明,在样本不均衡的情况下,该模型在实现白酒基酒等级分类中准确率达到96.61%,为面向不均衡数据集的白酒基酒分类提供了一种有效的方法。后续研究将从基酒中的各挥发性风味物质入手,探讨在均衡样本下基酒中各挥发性风味物质对基酒品质的影响,以进一步提高基于GC-MS技术的基酒等级分类模型的适用性。
[1]XU Y Q,ZHAO J R,LIU X,et al.Flavor mystery of Chinese traditional fermented Baijiu: The great contribution of ester compounds[J].Food Chem,2022,369:130920.
[2]胡景辉,陈禹锜,薛新新,等.浓香型白酒发展概述[J].中国酿造,2022,41(6):24-30.
[3]胡丽莎,戴怡凤,邱树毅.感官分析在白酒风味物质研究中的应用进展[J].食品与发酵科技,2022,58(5):101-106.
[4]邓高琼,陈亨业,刘瑞,等.气相色谱-质谱联用技术在食药检测中的应用与发展[J].化学试剂,2021,43(5):555-562.
[5]马凤丽,庞臻,曾英,等.红外光谱在白酒检测中的应用研究进展[J].酿酒科技,2022(5):103-107.
[6]罗琪,张贵宇,庹先国,等.电子鼻在成品白酒检测中的应用研究进展[J].粮食与油脂,2022,35(4):4-7.
[7]李坚,曾新安,郭时印.核磁共振技术在酒的质量检测中的应用[J].食品工业科技,2016,37(19):396-400.
[8]钱宇,胡雪,孙跃,等.基于指纹图谱和化学计量学的浓香型白酒分类研究[J].中国酿造,2021,40(6):152-156.
[9]陈明举,周迪,王鸿,等.基于GC-MS的浓香型白酒等级评判模型研究[J].中国酿造,2021,40(10):102-107.
[10]朱开宪,胡雪,邓静,等.基于GC-MS技术对不同香型白酒的判别分析[J].中国酿造,2023,42(1):213-218.
[11]王猛,赵华.中国白酒行业发展现状及趋势[J].酿酒,2022,49(1):39-41,46.
[12]宿晨,徐华,崔鑫,等.一种处理不均衡多分类问题的特征选择集成方法[J].重庆大学学报,2022,45(5):125-134.
[13] LIU B, TSOUMAKAS G.Dealing with class imbalance in classifier chains via random undersampling[J].Knowl-based Syst, 2020, 192:105292.
[14]HASANIN T,KHOSHGOFTAAR T M,LEEVY J L,et al.Severely imbalanced Big Data challenges: investigating data sampling approaches[J].J Big Data,2019,6(1):107.
[15] ELREEDY D,ATIYA A F.A comprehensive analysis of synthetic minority oversampling technique (SMOTE) for handling class imbalance[J].Inform Sci,2019,505:32-64.
[16]石洪波,陈雨文,陈鑫.SMOTE过采样及其改进算法研究综述[J].智能系统学报,2019,14(6):1073-1083.
[17]QUAN Y H,ZHONG X,FENG W,et al.SMOTE-based weighted deep rotation forest for the imbalanced hyperspectral data classification[J].Remote Sens,2021,13(3):464.
[18]张家伟,郭林明,杨晓梅.针对不平衡数据的过采样和随机森林改进算法[J].计算机工程与应用,2020,56(11):39-45.
[19]王磊,刘雨,刘志中,等.处理不平衡数据的聚类欠采样加权随机森林算法[J].计算机应用研究,2021,38(5):1398-1402.
[20]ZHOU Z H,FENG J.Deep forest[J].Natl Sci Rev,2019,6(1):74-86.
[21]韩云翠,吕志远,刘玉涛,等.基于气相色谱与支持向量机的浓香型白酒基酒等级判断模型研究[J].中国酿造,2023,42(5):184-190.
[22]FERRER C A,ARAGON E.Note on'a comprehensive analysis of synthetic minority oversampling technique(SMOTE)for handling class imbalance'[J].Inform Sci,2023,630:322-324.
[23]BARTH J,KATUMULLAGE D,YANG C Y,et al.Classification of wines using principal component analysis[J].J Wine Econ,2021,16(1):56-67.
[24]ZOU H,HASTIE T,TIBSHIRANI R.Sparse principal component analysis[J].J Comput Graph Stat,2006,15(2):265-286.
[25]杨赛华,周从华,蒋跃明,等.一种改进的不平衡数据过采样算法BNSMOTE[J].计算机与数字工程,2020,48(9):2108-2113.
[26]ZHU J,ZOU H,ROSSET S,et al.Multi-class Ada Boost[J].Stat Its Inter,2009,2(3):349-360.