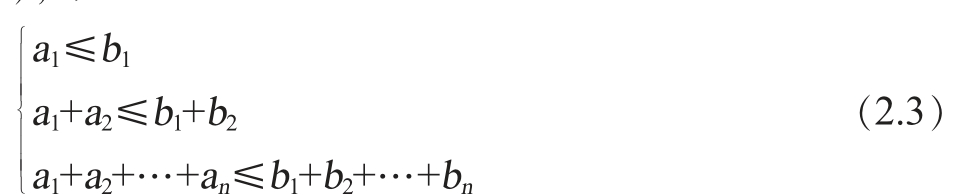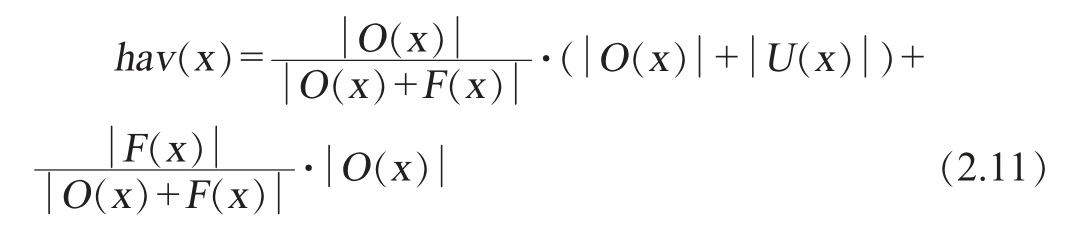Research on partial order set evaluation of financial performance of Baijiu enterprises:An empirical analysis based on Luzhou Laojiao
在中国经济高质量发展和消费结构升级的背景下，白酒作为中华传统文化的重要组成部分，不仅承载着厚重的历史文化底蕴，亦在国民经济中扮演着举足轻重的角色。伴随着市场竞争加剧和顾客需求多样化，白酒行业面临着前所未有的机遇与挑战，加之国家对白酒企业监管政策日趋完善，使得财务绩效评价不仅是内部管理的需要，更是外部合规的必然选择。“八项规定”提出以来，“三公消费”的限制力度逐步加大，一线白酒企业财务绩效较过往有了较大程度的下降[1]，如何有效评价和提升财务绩效，成为亟待解决的重要课题。2019年以来，供给侧结构性改革不断深化，白酒行业持续回暖，国家发展改革委颁布的《产业结构调整指导目录（2019年版）》将白酒产业限制性政策解除，提出了新的要求和指导意见[2]。白酒文化具有较强的区域性特征[3]，在数字化转型背景下，高水平产业集中化已成为白酒产业高质量发展的新趋势，因此需要更加精准地掌控财务绩效水平，以提高管理效率和企业核心竞争力。
综观企业财务绩效评价方面的研究，研究方法已相对成熟[4]。国内外学者主要采用熵权优劣解距离法（technique fororderpreferencebysimilaritytoanidealsolution，TOPSIS）[5]、因子分析法（factor analysis，FA）[6]、层次分析法（analytic hierarchy process，AHP）[7]、数据包络分析法（data envelopment analysis，DEA）[8]、灰色关联分析法（grey relation analysis，GRA）[9]等方法实施了财务绩效评价研究，均面临了不同程度的权重无法精确赋值的困扰。 值得一提的是，在岳立柱等[10]提出的“隐式”赋权偏序集决策方法基础上，陈亮等[11]基于偏序集理论，为商业银行财务绩效评价提供了新的视角和工具，通过指标重要性排序，克服了评价指标精确赋权问题。上述研究基于不同方法对财务绩效评价进行了较为深入的探讨，为本文研究提供了重要的理论来源和方法参考。同时，通过对现有文献的梳理和分析，发现白酒企业评价研究主要集中于企业绩效[2，12]、财务绩效[1]、销售业绩[13]、综合实力[14]、竞争力[15-16]、可持续发展[17]、综合效率[18]、质量[19]和科技创新水平[20]等，对财务绩效的深入研究相对较少。其中，王秋丽等[18]评价了中国白酒上市公司综合效率，揭示行业内资源浪费和产出不足问题；史利沙等[12]则构建了六个维度的评价指标体系，采用改进熵值法揭示了白酒企业的财务表现，为战略决策提供依据。
在白酒行业中，泸州老窖股份有限公司（以下简称“泸州老窖”）经营管理活动较为丰富，自1994年上市以来，经历了企业并购、多品类布局、数智化转型等一系列变革，其竞争优势[21]、高质量发展模式[22]、发展战略[23]等为学界和业界提供了丰富的研究案例。作为白酒行业龙头企业[21]，泸州老窖在2024全球十大最具实力烈酒品牌中，位居世界第五[24]，其财务绩效水平备受各界关注。鉴于此，本文以泸州老窖为主要研究对象，选用16家白酒上市公司作为研究样本，建立白酒企业财务绩效评价体系，基于偏序集决策方法实施综合评价，规避多指标评价权重赋值难题，以期揭示财务绩效提升的对策着力点，推动泸州老窖和白酒产业高质量发展。
财务指标选择是构建评价指标体系的首要环节，其数量和方向直接影响评价结果。依据指标设计的导向性原则、平衡性原则和可操作性原则[13]，本文根据国资委2024年发布的《企业效绩评价操作细则（修订）》，结合白酒上市公司特点，综合已有研究成果[25]，选定盈利能力、营运能力、偿债能力、发展能力4个一级指标；再以一级指标为基础，构建了净资产收益率、营业净利率、成本费用利润率、总资产净利率等12个二级指标，最终得到白酒企业财务绩效评价指标体系，结果见表1。
表1 白酒企业的财务绩效评价指标体系
Table 1 Financial performance evaluation indicator system of Baijiu enterprises
一级指标 二级指标 指标代码 计算公式A1净资产收益率= 净利润平均净资产盈利能力（A）A2营业净利率= 净利润营业收入净资产收益率营业净利率成本费用利润率总资产净利率总资产周转率应收账款周转率A3成本费用利润率= 利润总额成本费用总额A4总资产净利率=净利润总资产营运能力（B）B1 B2总周资产转率=销售收入总资产应收账款周转率=主营业务收入净额应收账款平均余额
续表
一级指标 二级指标 指标代码 计算公式存货周转率=销售（营业）成本平均存货资产负债率=负债总额资产总额偿债能力（C）存货周转率资产负债率速动比率B3 C1 C2速动比率=（流动资产-存货）流动负债流动比率=流动资产流动负债发展能力（D）流动比率营业收入增长率净利润增长率C3 D1营业收入增长率=本年营业收入增长额上年营业收入总额D2净利润增长率=净利润增加额上年净利润
在文献研究[5，25-28]的基础上，邀请5位专家对白酒企业财务绩效评价指标进行重要性排序，并对排序结果进行指标秩和计算[11]，秩和越小，指标重要性越大。指标重要性排序结果见表2。综上可确定一级指标重要性排序为：盈利能力＞营运能力＞偿债能力＞发展能力，即ω1＞ω2＞ω3＞ω4。
表2 指标重要性排序结果
Table 2 Ranking results of indicator importance
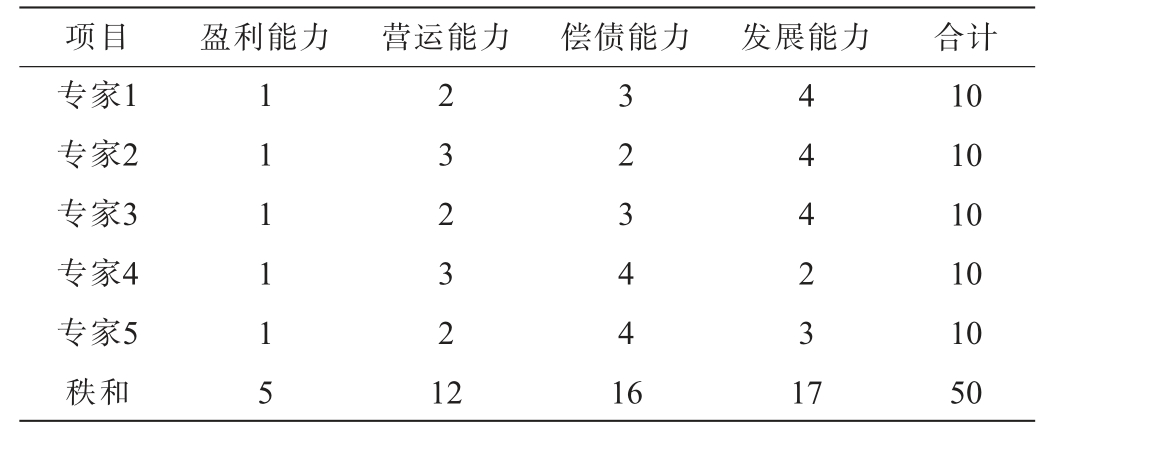
项目 盈利能力 营运能力 偿债能力 发展能力 合计专家1专家2专家3专家4专家5秩和1 1 1 1 1 5 2 3 2 3 2 1 2 3 2 3 4 4 1 6 4 4 4 2 3 1 7 10 10 10 10 10 50
定义1[10]设R是非空集合A上的一个二元关系，若R满足自反性、反对称性、传递性，则称R为A上的一个偏序关系。
（1）自反性：对任意x∈A，有xRx；
（2）反对称性：对任意x，y∈A，当xRy且yRx，有x=y；
（3）传递性：对任意x，y，z∈A，当xRy且yRz，有xRz。
则称R为A上的偏序关系。
定理1[30]给定评价集M=（A，IC，X），其中A={a1，…am}为评价方案集，IC={c1，c2，…cn}为准则集，X=（x1，x2，…，xm）T为初始评价矩阵，xi=（xi1，xi2，…，xim）∈Rn，其中xij表示方案ai在准则ci下的评价值。设准则权重ω1≥ω2≥…ωn≥0，若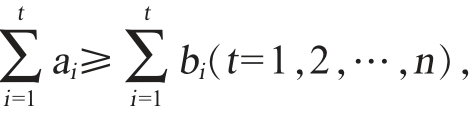
则g（a）≥g（b）。
其中，函数g为简单线性函数，即g（a）=ω1a1+ω2a2+ωnan。
定理1刻画了权重空间Λ={（ω1，ω2，ωn）|ω1≥ω2≥…ωn≥0}。其中Λ是满足一定约束的权重集合。于是有
对于任意的b=（b1，b2，…，bn），在权重空间Λ上二者的比较可以整理为：
根据式（2.2）可知，若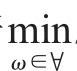
Δ（a，b）≥0，则对∀ω∈Λ，f（a1，a2，…，an）-f（b1，b2，…，bn）≥0。
对于任意ω∈Λ，当ai≥bi时，i=1，…，n，即根据单调性性质[7]可知f（a1，a2，…，an）≥f（b1，b2，…，bn）。
故集合Δ（a，b）={f（a1，a2，…，an）-f（b1，b2，…，bn）|ω∈Λ}中任意元素均≥0，进而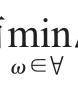
Δ（a，b）≥0。
（1）构建评价集
根据定理1，设定评价集为M=（A，IC，X）。 其中评价方案集为A={a1，…am}，准则集为IC={c1，c2，…，cn}，初始评价矩阵为X=（x1，x2，…，xm）T。
（2）构造偏序关系
由定理1可知，在权重空间Λ={（ω1，ω2，ωn）|ω1≥ω2≥…ωn≥0}内，若两个向量的关系满足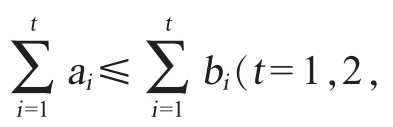
…，n），即
若式（2.3）成立，则有g（a）≤g（b），则该定理表明，两个简单线性加权函数的比较，并不一定需要精确的权重，仅仅需要权重的排序信息。 进一步研究表明，上述时（2.3）的比较可以转换成矩阵问题，即给定上三角矩阵E。
偏序关系即为方案的比较规则，利用偏序关系进行比较或排序，不仅能处理定比数据和定序数据，亦可将定性指标和定量指标共同集结，在一定程度上解决了指标权重赋值的难题，在应用范围上更加广泛。此外，在实施评价过程中通过融合专家经验，从而使得评价结果更加符合客观需求。
（3）建立比较关系矩阵
岳立柱等[10]提出用指标累加的方式将权重问题融入到方案评价过程中。评价指标重要性排序是偏序集决策方法的重要一环，综合1.2节指标重要性排序结果，获得的指标权重集为ω1≥ω2≥…≥ωn≥0。
对初始评价矩阵中的指标按照权重降序排列。为消除因指标数据间由数量级和量纲带来的影响，采用极差标准化方法对原始数据进行标准化预处理。
当ω1≥ω2≥…ωn≥0，上三角矩阵E和X进行如下运算，将前n个最重要指标累加，作为第n个指标，得到累加变换矩阵Y。
（4）建立HASSE矩阵，绘制HASSE图
由于偏序关系矩阵存在信息冗余，需要将其简化为HASSE矩阵HR。范懿[31]给出了二者的转换公式
式中：E为单位矩阵，运算符*为布尔运算。
根据式（2.6）建立比较关系矩阵R，通过式（2.7）转换得出HASSE矩阵。HASSE图是HASSE矩阵相互关联的图。根据HASSE矩阵绘制HASSE图。
（5）方案排序
偏序集决策方法在线性扩展集上构造了方案排序方法。 由HASSE图得到的全排序全体为线性拓展，在计算机科学中，获得偏序集线性拓展链的算法称为拓扑排序。 当指标涵盖的维度较大时，很难根据HASSE图计算理想状态下的所有扩展链。 因此，采用上集法和下集法在一定程度上解决了扩展链无法回答的问题[32]。
由评价集M=（A，IC，X）构造的偏序关系≤满足，对∀x，y∈A有
对于任意偏序集（A，≤），称集合O（x）={y∈A|x≥y}为A的下集；称集合F（x）={y∈A|x≤y}为A的上集；称集合U（A）为A的不可比集，其中：
令O（x） 、 F（x） 和U（x） 分别为O（x）、F（x）和U（x）元素个数，对有m个方案的偏序集（A，≤），其下集、上集和区间集元素个数满足
对于任意的x∈A方案在偏序集（A，≤）上的高度为
在评价过程中，偏序集方法根据评价过程中出现的hav（x）大小对方案进行排序[33-34]。
白酒企业所处的市场竞争环境错综复杂，动态性显著，且伴随持续的技术革新，使得指标权重在情境变迁中呈现不稳定性。敏感性指标可能对企业未来经营效益带来重要影响，因此识别影响企业财务绩效的敏感性指标尤为必要。敏感性分析有助于识别企业在哪些关键评价维度上的变动可能对其在行业竞争中的地位构成影响，进而威胁其战略发展的稳定性。
现行的敏感性分析方法，主要为局部敏感性分析[35]，呈现出偏静态特征，即假设其他指标权重不变，某个指标权重变动对总排序的影响。考虑到实际情境中指标变化的动态特征，本文基于偏序集视角，构造全局特征的动态敏感性分析方法。
设存在n个指标权重，敏感性分析中权重变动量Δ，则第i个准则权重变动后的表达式为
式中：wi为变动前权重，ωi为变动后的权重
初始权重向量
对其他指标权重ωi，j≠i，j=1，…，n，有
（1）构建权重空间
敏感程度与权重变动范围有关，无论初始权重大小，随着情境的变化其重要性均可能发生剧烈翻转。为此，对准则权重变动给出两种状态：
①主要准则权重取最大，其他准则权重任意变动，权重向量集合称之为极大权重空间，表达式为
②主要准则权重取最小，其他准则权重任意变动，权重向量集合称之为极小权重空间，表达式为
极大、极小权重空间代替权重变动的上下界，分别刻画了主要准则权重在最大和最小情境下所有权重变动的可能。
（2）方案及指标敏感度
若某一指标无论权重值如何变化，方案排序均不变，则该指标为非敏感指标；相反若方案排序变动明显，则为敏感性指标。令Jj （ai）表示权重ωi取最大时，方案ai的排序区间均值；令Jj （ai）为表示权重ωj取最小时，方案ai的排序区间均值。指标j的权重两极转换过程中，排序变动差的绝对值为
指标j对所有方案序值差值的和为dj
方案ai在对所有指标序值差值的和为Si
指标j敏感度为βj
βj越大表明指标j相对于其他指标的敏感程度越高。
方案ai关于指标j的敏感度为aij
方案ai敏感度为λi
λi越大表明方案相ai对于其他方案的敏感程度越高。无论是方案敏感度还是指标敏感度，取值越大表示敏感程度越高。
中国证监会白酒上市公司名单中主营业务为白酒酿造的企业共计19家，排除ST及数据缺失、数据值异常的公司，本文选取泸州老窖等代表性上市白酒企业16家，数据来源于东方财富网、新浪财经网及各白酒上市企业年报等。A股样本白酒企业，见表3。
表3 白酒上市企业及样本编号
Table 3 Listed Baijiu enterprises and sample number
序号 名称 序号 名称C01 C02 C03 C04 C05 C06 C07 C08泸州老窖古井贡酒酒鬼酒五粮液顺鑫农业洋河股份伊力特金种子C09 C10 C11 C12 C13 C14 C15 C16贵州茅台老白干酒水井坊山西汾酒迎驾贡酒今世缘口子窖金徽酒
根据1.1节白酒企业财务绩效评价指标体系，构建评价集M；将二级指标划分为效益型指标和成本型指标，依据样本白酒企业2019-2023年财务数据，进行归一化及成本型指标调整处理，获得初始评价矩阵X，见表4，并构造偏序关系。
表4 初始评价矩阵X
Table 4 Initial evaluation matrix X
项目 A1 A2 A3 A4 B1 B2 B3 C1 C2 C3 D1 D2 C01 C02 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C13 C14 C15 C16 0.789 0.518 0.520 0.747 0.009 0.533 0.286-0.109 1.000 0.256 0.767 0.804 0.648 0.591 0.591 0.329 0.768 0.508 0.503 0.646 0.021 0.506 0.248-0.096 0.832 0.330 1.000 0.966 0.609 0.582 0.518 0.276 0.723 0.380 0.452 0.710 0.001 0.607 0.311-0.177 1.000 0.215 0.479 0.499 0.566 0.593 0.620 0.308 0.481 0.169 0.216 0.451 0.014 0.317 0.136-0.030 1.000 0.079 0.235 0.259 0.293 0.306 0.349 0.114 0.187 0.006 0.001 0.007 0.002 0.002 0.001 0.000 0.025 0.001 0.030 1.000 0.004 0.007 0.000 0.006 0.684 0.849 0.707 0.655 0.837 0.549 0.556 0.405 0.641 0.743 1.000 0.996 0.709 0.621 0.593 0.672 0.371 0.512 0.320 0.763 1.000 0.287 0.618 0.479 0.194 0.461 0.228 0.465 0.307 0.378 0.265 0.417 0.724 0.576 0.660 0.922 0.357 0.601 0.853 0.755 1.000 0.295 0.333 0.442 0.626 0.482 0.670 0.614 0.649 0.504 0.540 0.975 0.269 0.460 0.540 0.454 1.000 0.168 0.189 0.341 0.355 0.388 0.391 0.278 0.458 0.462 0.506 0.613 0.000 0.507 0.625 0.588 0.665 0.210 0.190 0.271 0.514 0.447 0.606 0.646 0.663 0.680 0.887 0.570-0.053 0.258 0.111 0.155 0.514 0.303 0.513 1.000 0.536 0.801 0.279 0.431 0.621 0.487 0.700 0.362-3.476 0.153 0.226-5.504 0.327 0.351 0.373 1.000 0.532 0.476 0.086 0.133
将初始评价矩阵X中二级指标转换为一级指标，按照指标权重降序排列，进而进行累加变换，获取累加评价矩阵Y，见表5。
表5 累加评价矩阵Y
Table 5 Cumulative evaluation matrix Y
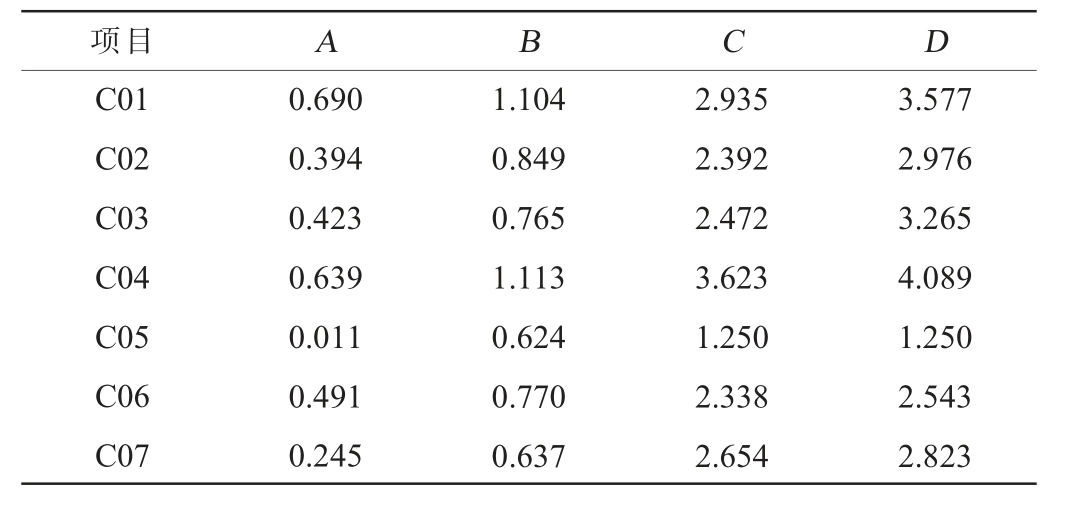
项目 A B C D C01 C02 C03 C04 C05 C06 C07 0.690 0.394 0.423 0.639 0.011 0.491 0.245 1.104 0.849 0.765 1.113 0.624 0.770 0.637 2.935 2.392 2.472 3.623 1.250 2.338 2.654 3.577 2.976 3.265 4.089 1.250 2.543 2.823
续表
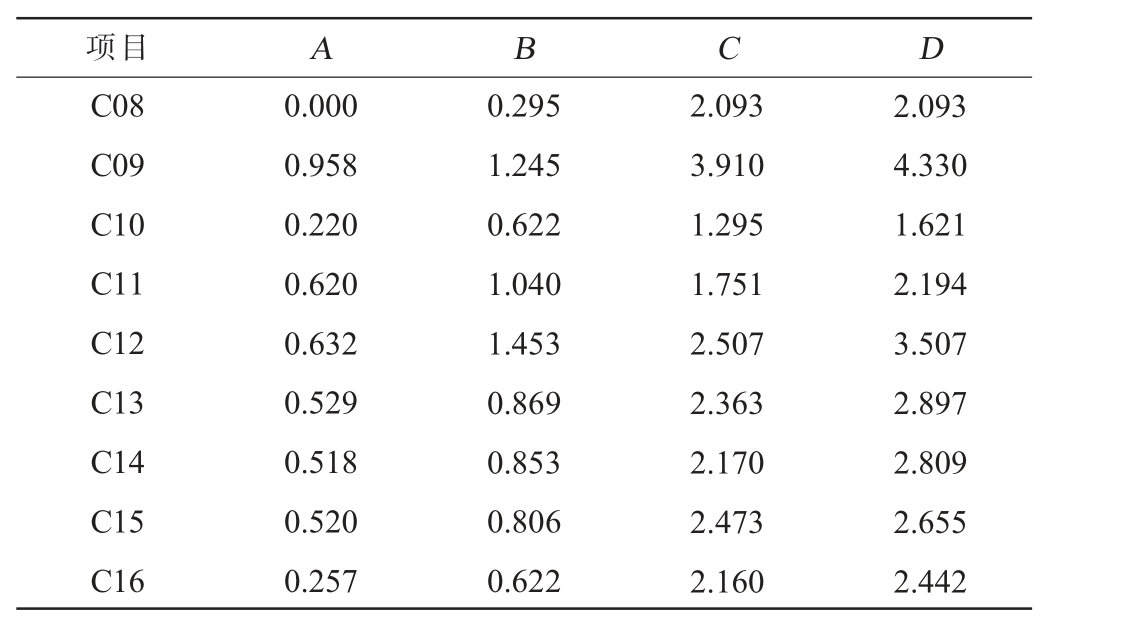
项目 A B C D C08 C09 C10 C11 C12 C13 C14 C15 C16 0.000 0.958 0.220 0.620 0.632 0.529 0.518 0.520 0.257 0.295 1.245 0.622 1.040 1.453 0.869 0.853 0.806 0.622 2.093 3.910 1.295 1.751 2.507 2.363 2.170 2.473 2.160 2.093 4.330 1.621 2.194 3.507 2.897 2.809 2.655 2.442
在累加评价矩阵Y的基础上，进行行行比较，建立比较关系矩阵R，见表6。
表6 比较关系矩阵R
Table 6 Comparison relation matrix R
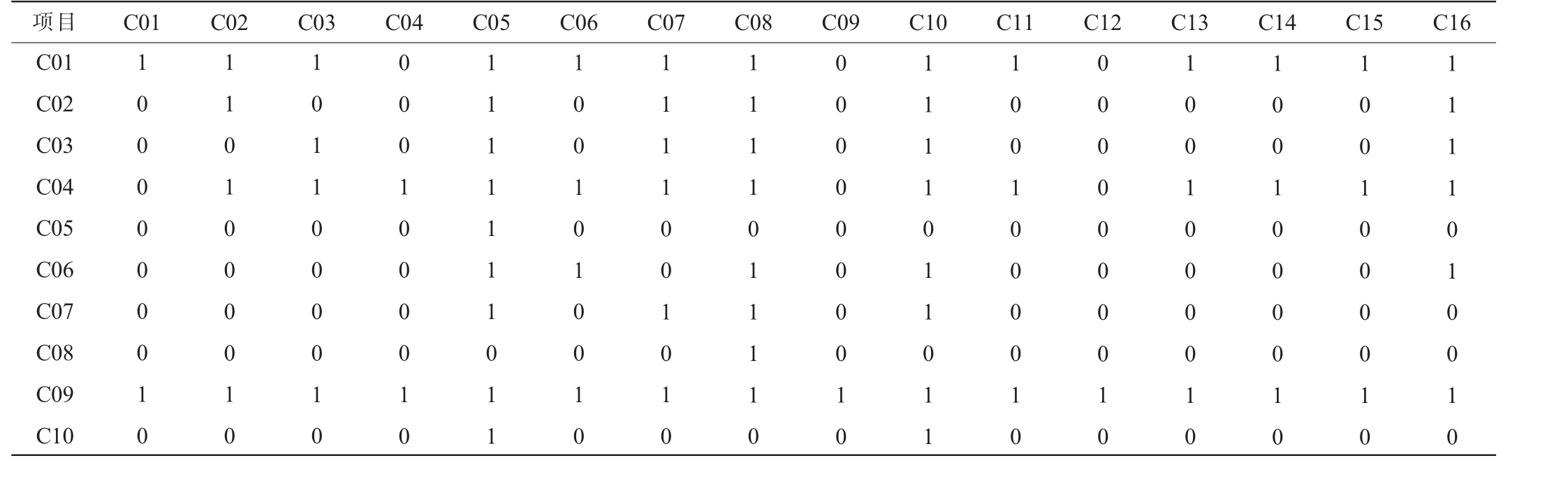
项目 C01 C02 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C13 C14 C15 C16 C01 C02 C03 C04 C05 C06 C07 C08 C09 C10 1 0 0 0 0 0 0 0 1 0 1 1 0 1 0 0 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 1 1 0 1 1 1 0 0 1 0 1 0 0 1 0 1 1 1 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 0 1 0
续表
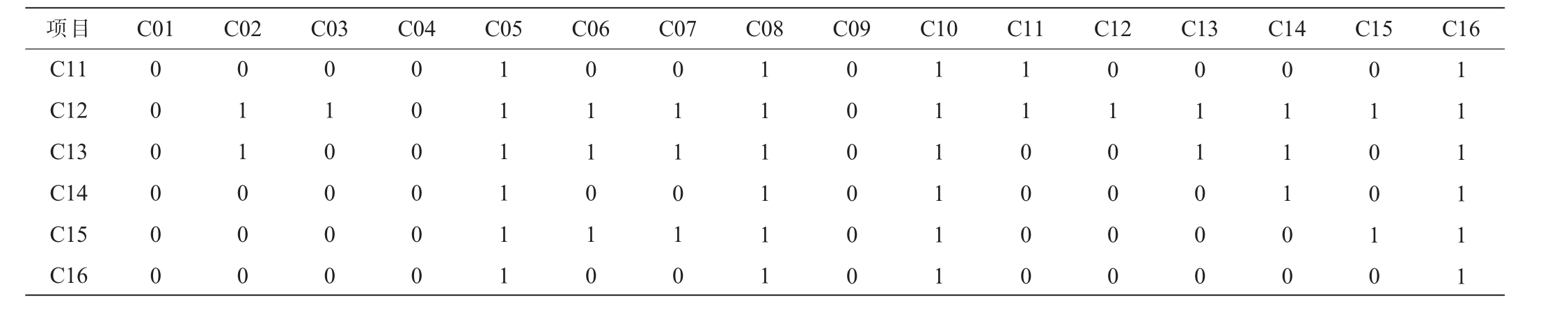
项目 C01 C02 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C13 C14 C15 C16 C11 C12 C13 C14 C15 C16 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 1 0 1 1 1 1 1 1
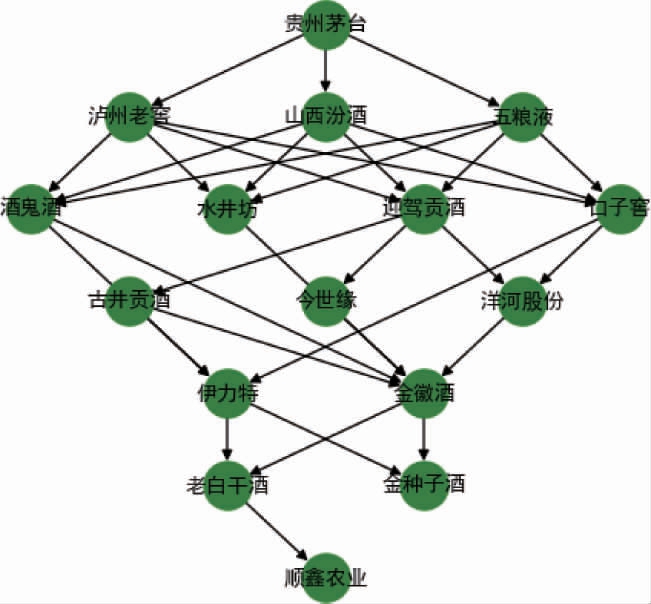
将比较关系矩阵转换为HASSE矩阵，绘制白酒企业财务绩效HASSE图，如图1所示。
图1 白酒企业财务绩效HASSE图
Fig.1 HASSE diagram of financial performance of Baijiu enterprises
（1）方案排序
按照比较关系矩阵，计算各白酒企业财务绩效秩均值，对HASSE图各层集元素进行排序，见表7。
表7 白酒企业2019-2023年秩均值排序
Table 7 Ranking of rank average values of Baijiu enterprises in 2019-2023
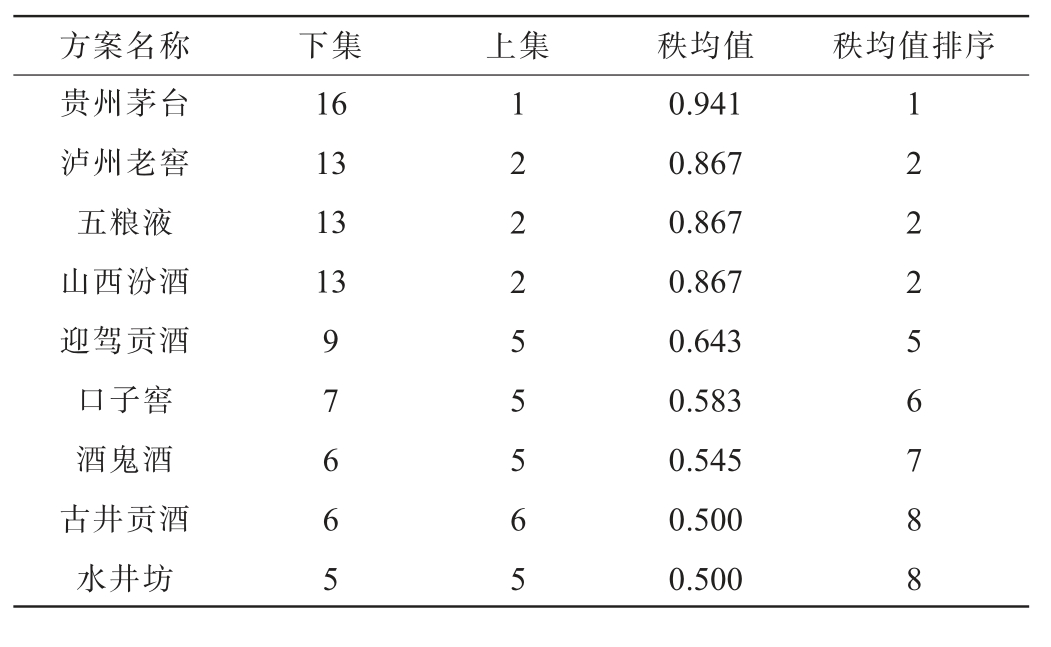
方案名称 下集 上集 秩均值 秩均值排序贵州茅台泸州老窖五粮液山西汾酒迎驾贡酒口子窖酒鬼酒古井贡酒水井坊16 13 13 13 9 7 6 6 5 1 2 2 2 5 5 5 6 5 0.941 0.867 0.867 0.867 0.643 0.583 0.545 0.500 0.500 1 2 2 2 5 6 7 8 8
续表
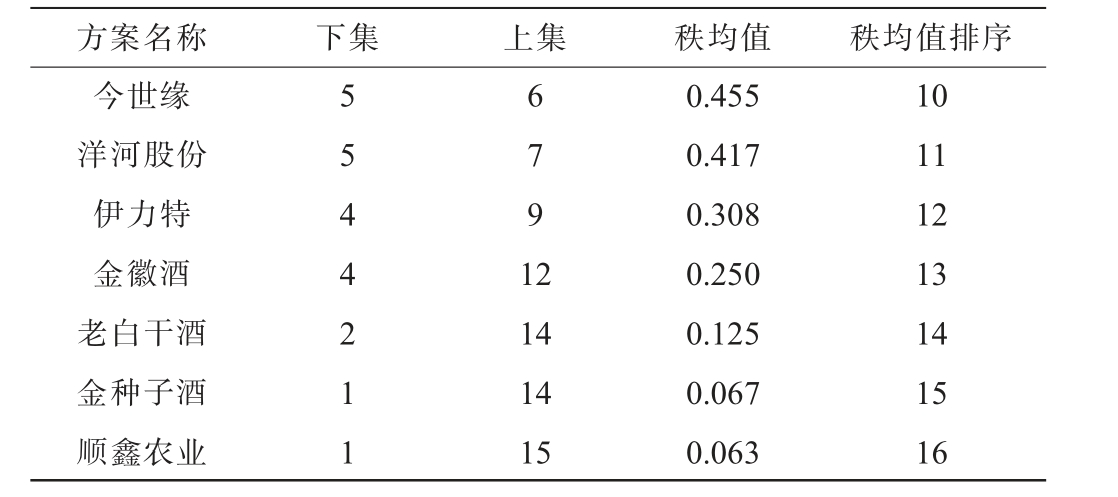
方案名称 下集 上集 秩均值 秩均值排序今世缘洋河股份伊力特金徽酒老白干酒金种子酒顺鑫农业5 5 4 4 2 1 1 6 7 9 1 2 14 14 15 0.455 0.417 0.308 0.250 0.125 0.067 0.063 10 11 12 13 14 15 16
由表7可知，贵州茅台秩均值处于最高水平，为0.941；泸州老窖、五粮液及山西汾酒位列第二，均为0.867；迎驾贡酒为0.643，口子窖为0.583，酒鬼酒为0.545，古井贡酒和水井坊为0.5；剩余样本企业秩均值均＜0.5。
（2）HASSE图结构化诠释
由图1可知，16家白酒上市公司分为七层。结合表7，以hav（x）值0.5为界[36]将其分为两个等级，第一等级包含9家企业，第二等级包含7家企业，两个等级的财务绩效水平存在较大差异。进一步地，对16家白酒企业进行有效聚类，分为五个层集。第一层集{贵州茅台、泸州老窖、五粮液、山西汾酒}；第二层集{迎驾贡酒、口子窖、酒鬼酒、古井贡酒、水井坊}；第三层集{今世缘、洋河股份}；第四层集{伊力特、金徽酒}；第五层集{老白干酒、金种子酒、顺鑫农业}。
（3）竞争态势解析
HASSE图的纵向关系体现方案间的层集信息，横向关系则体现同层集内方案聚类信息。 结合图1和表7，从全局视角进一步审视，HASSE图中箭头连接的白酒企业之间，财务绩效存在直接的可比关系，箭头之前的白酒企业在盈利能力、营运能力等方面优于箭头之后的白酒企业，排序具备相对稳定性；HASSE图中非箭头连接的白酒企业之间，上层集白酒企业对下层集白酒企业未必拥有直接的优势，排序不具备相对稳定性。同时，HASSE图揭示了白酒企业的竞争态势。HASSE图中箭头指向可衡量样本企业在市场竞争中的“侵占性”，箭头指向其他样本企业的数量越多，反映出该白酒企业市场扩张态势越强；反之，若白酒企业被其他样本企业箭头指向越多，则表明其在市场环境中面临更多的被侵占风险。
具体而言，位于HASSE图顶端的第一层集企业，贵州茅台均未受到其他白酒企业的箭头指向，反映其财务绩效具有绝对优势，泸州老窖、五粮液及山西汾酒3家企业均受到来自贵州茅台的箭头指向，表明贵州茅台对3家企业拥有直接的竞争优势。 同时，这些企业均具备指向其他企业的箭头，显示其在竞争态势上表现出较强的主动性。 第二至第四层集的样本企业相较于第一层集企业，其竞争态势稍显薄弱。 值得注意的是，这三个层集的企业均受到来自上一层集企业的箭头指向，说明其面临着高层集企业的侵占风险。 第一和第二层集的企业呈现较多的箭头交互，折射出相关层集白酒企业之间复杂的竞争态势。第五层集的顺鑫农业位于HASSE图底部，无任何指向其他企业的箭头，表明该企业在市场环境缺乏侵占性。
泸州老窖位于HASSE图的第一层集，其财务绩效水平仅次于贵州茅台，在图1中仅被1家企业箭头指向，且泸州老窖箭头指向了4家企业，反映出其竞争态势较强。结合白酒上市企业年报数据分析可知，尽管泸州老窖在行业内展现出显著的竞争优势，但仍面临着一定的财务压力，尤其在偿债能力方面有较大提升空间。 因此，泸州老窖应在稳固现有竞争态势的基础上，积极改善其经营策略，全面提升财务绩效水平。
鉴于泸州老窖的市场竞争态势较为复杂，指标权重在情境变迁中动态性显著。因此对泸州老窖财务绩效实施偏序动态敏感性分析，以增强决策过程的科学性，为规避潜在风险和制定战略计划提供有力依据。选取2019-2023年泸州老窖及样本企业财务指标数据，针对盈利能力、营运能力、偿债能力和发展能力四类一级指标进行偏序动态敏感性分析。
（1）一级指标数据表
剔除盈利能力指标的累加数据，得到盈利能力敏感性分析数据，见表8。
表8 盈利能力敏感性分析数据
Table 8 Profitability sensitivity analysis data
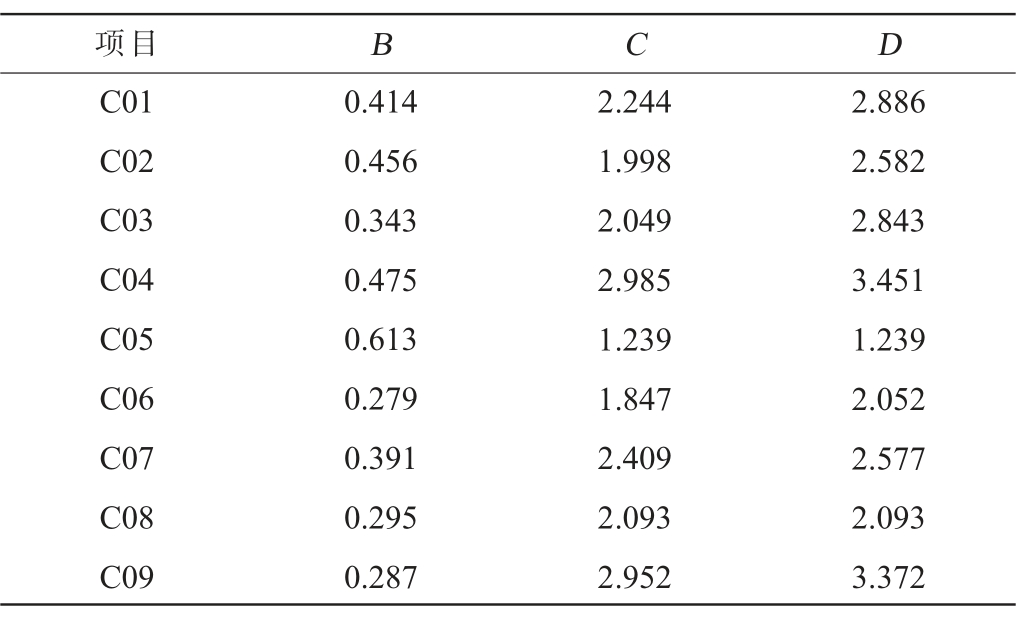
项目 B C D C01 C02 C03 C04 C05 C06 C07 C08 C09 0.414 0.456 0.343 0.475 0.613 0.279 0.391 0.295 0.287 2.244 1.998 2.049 2.985 1.239 1.847 2.409 2.093 2.952 2.886 2.582 2.843 3.451 1.239 2.052 2.577 2.093 3.372
续表
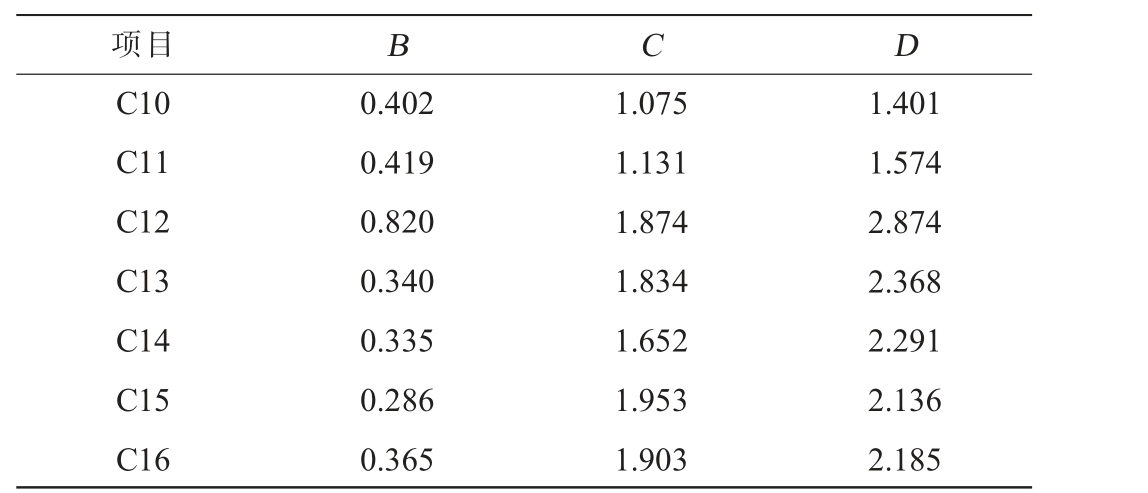
项目 B C D C10 C11 C12 C13 C14 C15 C16 0.402 0.419 0.820 0.340 0.335 0.286 0.365 1.075 1.131 1.874 1.834 1.652 1.953 1.903 1.401 1.574 2.874 2.368 2.291 2.136 2.185
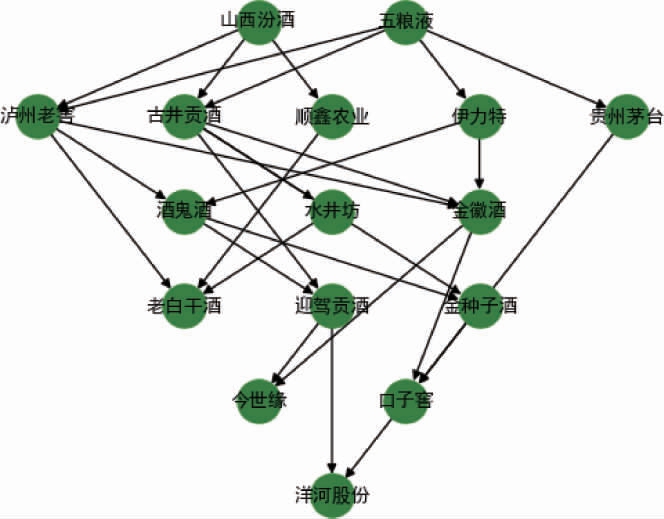
（2）敏感性HASSE图
基于偏序集决策方法，分析盈利能力的动态敏感性，得到其动态敏感性HASSE图，如图2所示。同理分别得到营运能力、偿债能力和发展能力的动态敏感性HASSE图。
图2 盈利能力动态敏感性HASSE图
Fig.2 HASSE diagram of dynamic sensitivity of profitability
（3）方案排序
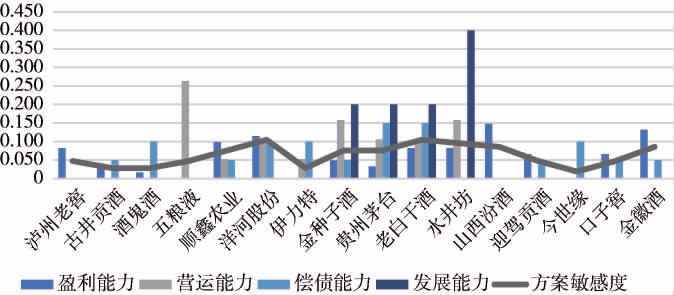
根据比较关系矩阵和动态敏感性HASSE图，得到白酒企业分别关于四类指标敏感度、四类指标整体敏感度及各企业敏感度，见表9，变化趋势见图3。
图3 白酒企业财务绩效指标敏感度变化趋势
Fig.3 Sensitivity change trend of financial performance indicators of Baijiu enterprises
表9 白酒企业财务绩效指标敏感度
Table 9 Sensitivity of financial performance indicators of Baijiu enterprises
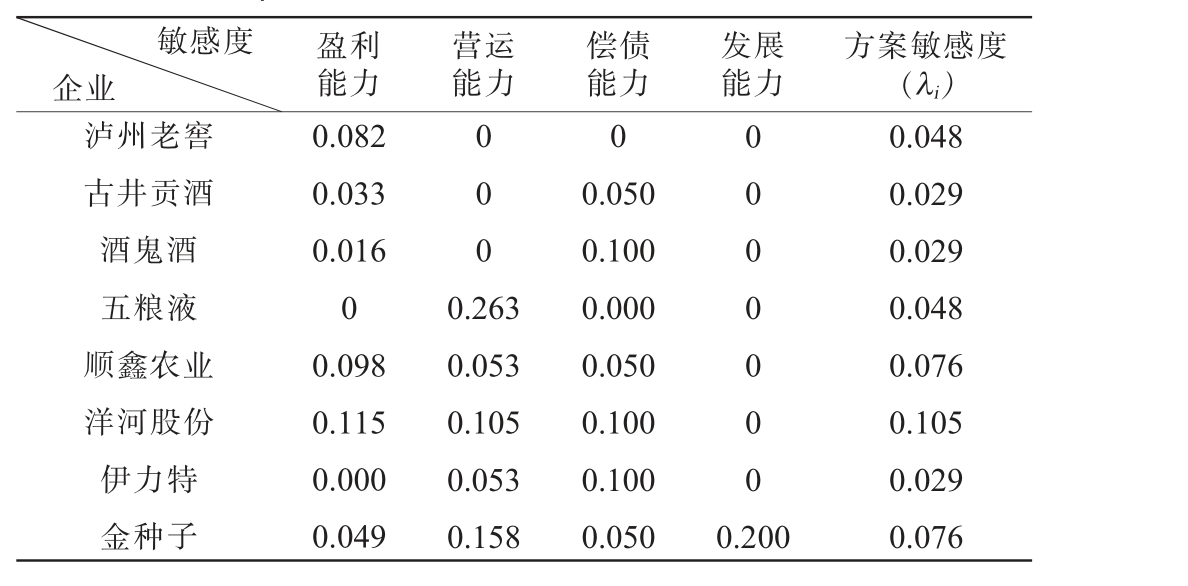
敏感度企业盈利能力营运能力偿债能力发展能力方案敏感度（λi）泸州老窖古井贡酒酒鬼酒五粮液顺鑫农业洋河股份伊力特金种子0.082 0.033 0.016 0 0.098 0.115 0.000 0.049 000 0 0.263 0.053 0.105 0.053 0.158 0.050 0.100 0.000 0.050 0.100 0.100 0.050 0000 000 0.200 0.048 0.029 0.029 0.048 0.076 0.105 0.029 0.076
续表
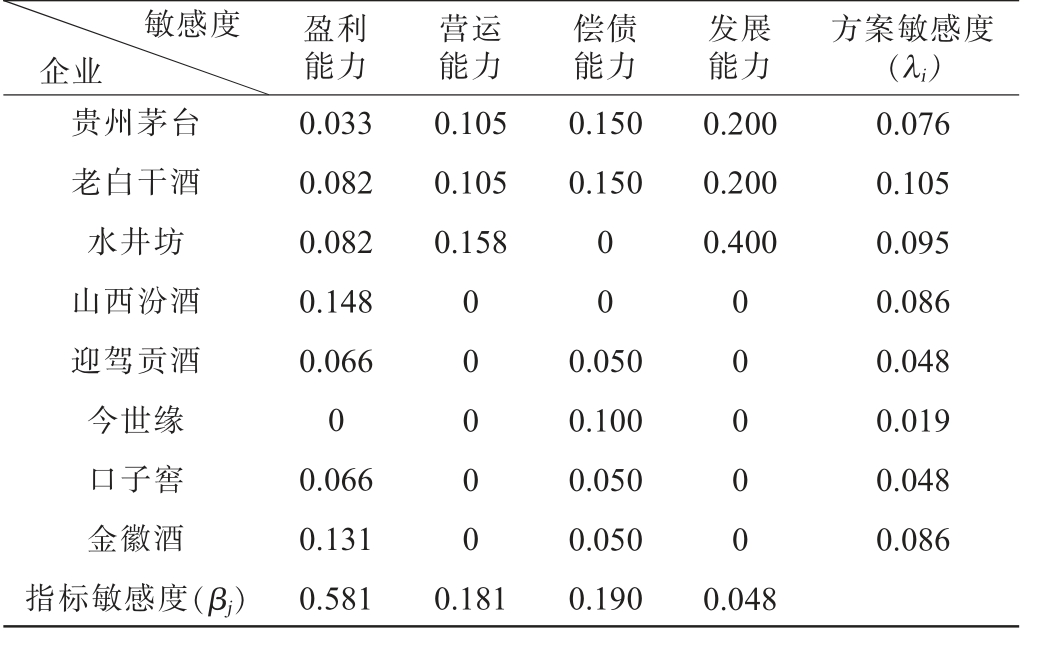
敏感度企业盈利能力营运能力偿债能力发展能力方案敏感度（λi）贵州茅台老白干酒水井坊山西汾酒迎驾贡酒今世缘口子窖金徽酒指标敏感度（βj）0.033 0.082 0.082 0.148 0.066 0 0.066 0.131 0.581 0.105 0.105 0.158 0.150 0.150 0.200 0.200 0.400 0 0 0 0 0 0 0 0 0 0 0 0 0.076 0.105 0.095 0.086 0.048 0.019 0.048 0.086 0.181 0.050 0.100 0.050 0.050 0.190 0.048
由表9及图3可知，整体指标敏感度最大的方案集为{洋河股份、老白干酒}；其中，盈利能力指标敏感度最大的方案集为{山西汾酒、金徽酒、洋河股份}；营运能力对应敏感度最大的方案集为{五粮液、金种子酒、水井坊}；偿债能力对应的敏感度最大的方案集为{贵州茅台、老白干酒}；发展能力对应的敏感度最大的方案集为{水井坊}。
对样本企业的方案敏感性而言，泸州老窖敏感度为0.048，排序在16家样本企业中与五粮液、迎驾贡酒和口子窖并列，位列第9，表明泸州老窖在行业中排序较为稳定，不易出现排序波动。泸州老窖财务绩效指标敏感度，见表10。
表10 泸州老窖财务绩效指标敏感度
Table 10 Sensitivity of financial performance indicators of Luzhou Laojiao
项目 盈利能力 营运能力 偿债能力 发展能力 方案敏感度敏感度排名0.082 5 0 9 0 13 0 5 0.048 9
综合上述图表进一步分析，泸州老窖盈利能力指标的敏感度最为显著，而营运能力、偿债能力和发展能力则呈现出相对较低的敏感度。 尽管营运能力、偿债能力和发展能力在稳定性方面表现良好，且敏感度低于多数白酒企业，但盈利能力敏感度较高，为起主要决定作用的关键影响因素，揭示了财务绩效提升对策的着力点。
针对白酒企业财务绩效评价问题，本文选择泸州老窖为主要研究对象，以16家白酒上市公司为样本，采用偏序集决策方法实施了财务绩效评价，归纳概括如下结论：
（1）提出了契合白酒企业经营特点的财务绩效偏序集评价方法。本文首次在白酒企业财务绩效评价中引入偏序集决策方法，通过指标重要性排序实现指标集结，规避了指标难以精确赋权的问题，获得了更准确的样本企业财务绩效排序，形成兼具普适性和稳健性的财务绩效评价模式，弥补了传统评价方法的不足。
（2）分析了白酒企业财务绩效的HASSE图竞争态势。HASSE图纵向关系体现方案间的层集信息，横向关系则体现同层集内方案聚类信息。HASSE图箭头连接的白酒企业之间，财务绩效存在直接的可比关系，箭头之前的白酒企业在盈利能力、营运能力等方面优于箭头之后的白酒企业，排序具备相对稳定性，揭示了白酒企业的市场竞争态势，箭头数量可衡量态势强度。分析表明，泸州老窖位于HASSE图的第一层集，其财务绩效水平仅次于贵州茅台，且泸州老窖箭头指向了4家企业，反映出优越的竞争态势。
（3）识别了对白酒企业财务绩效起主要决定作用的关键影响因素。本文首次在白酒企业财务绩效评价中引入偏序动态敏感性分析方法，增强了多准则决策过程的科学性和精确性。 根据比较关系矩阵和动态敏感性HASSE图，得到相关敏感度及其变化趋势，有效识别了财务绩效关键影响指标。 结果表明，泸州老窖的盈利能力为起主要决定作用的关键影响因素，揭示了财务绩效提升对策的着力点。
基于财务绩效评价结果与关键影响因素，提出泸州老窖财务绩效提升的对策建议：
（1）全面提升盈利能力。根据3.6节的分析结论，泸州老窖的盈利能力为起主要决定作用的关键影响因素。因此，应基于领先行业的数字化改革进一步完善盈利模式，推进营销数字化、供应链数字化、酿酒数字化、管理数字化，使企业的资产管理水平和资产结构得到改善，提升总资产净利率和净资产收益率；强化核心业务，全品系推进“五码合一”工程，逐步构建核心数据源，全面提高以市场为导向的经营管理效率，促进“质量优化”的产品竞争和真实动销，提高营业净利率；优化成本结构，精确掌控盈亏平衡点，提高成本费用利润率；根据市场需求调整产品结构，实现白酒产品溢价，收获可持续、长远的净利润。
（2）全面提升营运能力。在酒业新周期，泸州老窖应基于“知名产区、著名品牌、优秀文化、优良品质”，持续加强智能化科研攻关，加快构建新质生产力；将大数据分析、智能决策、工业机器人等技术创新应用到技改项目中，提高资产周转率，突破白酒产业数字化转型的关键瓶颈；基于供应链视角，强化营销和渠道数智化改革，通过搭建消费者全生命周期运营管理模型和会员运营体系，进一步改善销售队伍团队效能，加强库存管理，提高存货周转率和应收账款周转率，规避牛鞭效应。
（3）全面提升偿债能力。3.5节分析表明，泸州老窖在偿债能力方面有较大提升空间，因此结合HASSE图竞争态势，积极应对市场变化，持续提升行业龙头的抗压能力与发展韧性，通过强化产品质量、降低成本、优化库存管理等策略提高速动比率和流动比率，有效增加市场份额；以推动“数智泸州老窖”建设为契机，结合企业数字化转型建立健全财务管理制度，确保资金能够科学用于掌控利润回报和稳步增值的白酒产品上，进而合理控制资产负债率，降低偿债风险，并将其内化到财务竞争力中，确保泸州老窖的偿债能力显著提升。
（4）全面提升发展能力。 作为大型国有企业和大型骨干酿酒企业，泸州老窖应基于“地、窖、艺、曲、水、粮、洞”核心资源，通过智能化改造与数字化转型驱动企业有效构建新的核心竞争力，提升品牌价值，强化产品动销转化，提高营业收入增长率；促进老字号企业组织变革，基于渠道和公司长期利益，推动种植、采购、酿造、包装、仓储、运输、配送和营销体系的数字化场景构造，形成“从田间到舌尖”的全产业链质量管理模式的迭代，进一步提高净利润增长率；以特色“浓香鼻祖”白酒文化推动酒旅融合新发展[37]，通过整合或协调利益相关者的行为共同实现竞争态势优化，确保业绩稳定增长，最大限度提升发展能力。
[1]王霞，王竞达.“八项规定”对酒类上市公司财务绩效的影响研究[J].经济与管理研究，2015，36（1）：139-144.
[2]陈一君，胡文莉，武志霞.白酒企业绩效评价指标体系构建与评价方法——基于BSC和熵权的改进TOPSIS模型[J].四川轻化工大学学报（社会科学版），2020，35 （5）：68-87.
[3]李明宇.中国白酒文化特征要素分析与内涵理论模型[J].中国酿造，2023，42（5）：248-254.
[4]SURKOVA E V,MAZHAISKII Y A.Assessing the financial performance of aviation enterprises[J].Russ Eng Res,2021,41(10):983-986.
[5]ZHANG S,LIU S,FANG Z,et al.Generalized grey information entropy weight TOPSIS model for financial performance evaluation considering differentiation[J].Kybernetes,2023,52(11):5412-5426.
[6]侯向鼎.A股上市物流供应链企业财务绩效评价——基于因子分析法[J].山西财经大学学报，2021，43（S2）：53-57.
[7]LI X,GAO H X,ZHOU E Y.Research on optimization of financial performance evaluation of energy enterprises under the background of lowcarbon economy[J].Energies,2024,17(10):2311.
[8]NEVES M E, HENRIQUES C, VILAS J.Financial performance assessment of electricity companies:Evidence from Portugal[J].Oper Res,2021,21(4):2809-2857.
[9]SUVVARI A, RAJA SETHU DURAI S, GOYARI P.Financial performance assessment using Grey relational analysis(GRA):An application to life insurance companies in India[J].Grey Syst,2019,9(4):502-516.
[10]岳立柱，张志杰，闫艳.蕴含权重的偏序集多准则决策法[J].运筹与管理，2018，27（2）：26-31.
[11]陈亮，刘欣慧，李春友.基于偏序集理论的商业银行财务绩效评价[J].统计与决策，2019，35（20）：178-181.
[12]史利沙，陈红.基于改进熵值法的白酒上市公司业绩评价[J].会计之友，2015（10）：25-28.
[13]李明宇.大型商超白酒销售业绩评价指标体系构建与应用研究[J].中国酿造，2023，42（10）：256-262.
[14]张鹏博，丁志伟，邱永宽.河南省品牌豫酒的实力差异与空间影响力研究[J].河南大学学报（自然科学版），2024，54（1）：15-29.
[15]廖斌，王婷，王海天.白酒企业可持续竞争力评价研究[J].中国酿造，2019，38（7）：200-204.
[16]谭宏.基于地域特征的中国传统白酒产业核心竞争力的构建[J].企业经济，2010（9）：93-96.
[17]李学华.白酒行业可持续发展状况评价研究——以典型白酒企业为例[J].中国酿造，2023，42（6）：262-268.
[18]王秋丽，陈谨.白酒上市公司综合效率分析[J].中国管理科学，2014，22（S1）：610-616.
[19]LIU Y,QIAO Z,ZHAO Z,et al.Comprehensive evaluation of Luzhouflavor liquor quality based on fuzzy mathematics and principal component analysis[J].Food Sci Nutr,2022,10(6):1780-1788.
[20]武志霞，郑霞忠，陈一君，等.科技创新与白酒产业高质量发展耦合协调研究[J].中国酿造，2024，43（9）：266-270.
[21]程虹，郭超然.资源编排视角下企业质量资源转化为竞争优势的内在机理——来自“泸州老窖”的案例[J].宏观质量研究，2024，12（1）：1-14.
[22]何诚，陈凯，杜娟.泸州老窖“一核三驱动”的高质量发展模式[J].宏观质量研究，2023，11（4）：12-23.
[23]安宁.泸州老窖：向“新”而行 数智赋能引领酒业更高质量发展[N].四川日报，2024-05-31.
[24]BRAND FINANCE.Brand Finance Alcoholic Drinks 2024 Report[EB/OL].https://brandirectory.com/rankings/spirits,2024-06-28.
[25]姚文韵，陈榕.财务管理[M].北京：高等教育出版社，2024：58-69.
[26]张红霞，逯程玲.基于熵权法的高新技术企业财务绩效评价研究——以万润科技为例[J].会计之友，2023（12）：80-88.
[27]郝艳华.基于AHP-DEA模型的饲料上市公司财务绩效评价研究[J].饲料研究，2022，45（4）：123-127.
[28]蔡立新，高蔓莉.国有资本投资公司财务绩效评价[J].财会月刊，2021（1）：44-51.
[29]LI M Y,XU R Z,CHEN Q H.A partial order OWA operator for solving the OWA weighing dilemma[J].IEEE Access,2023,11:55435-55441.
[30]岳立柱，李良琼.应用偏序集表示权重难以获知的TOPSIS模型[J].模糊系统与数学，2017，31（4）：167-174.
[31]范懿.一个有关哈斯图的解析方法[J].上海第二工业大学学报，2003（1）：17-22.
[32]李明宇，岳立柱，金珊.应用关系矩阵表示偏序集平均高度的方法[J].辽宁工程技术大学学报（自然科学版），2018，37（1）：216-220.
[33]BRUGGEMANN R, ANNONI P.Average heights in partially ordered sets[J].Match Commun Math Comput Chem,2014,71(1):117-142.
[34]李明宇.大型商超白酒产品促销效能评价方法研究[J].中国酿造，2023，42（9）：246-252.
[35]罗勇，王森.管理会计的若干工具在财务公司应用的几点思路——以某集团财务公司为例[J].中国注册会计师，2019（5）：101-105.
[36]李明宇.大型商超白酒销售业绩影响因素研究[D].阜新：辽宁工程技术大学，2021.
[37]李明宇.白酒文化推动酒旅融合发展作用机理及实现路径——基于李渡酒业的案例分析[J].中国酿造，2024，43（10）：288-297.