为0.983 1，验证集的决定系数
为0.967 3，残差预测偏差（RPD）为5.602 1，表现出较好的预测能力；此外，一阶导数结合SVR模型也显示出较高的预测精度，训练集的决定系数
为0.971 2，验证集的决定系数
为0.980 5，残差预测偏差（RPD）为7.257 3。综上，基于近红外光谱与机器学习结合的方法能够有效预测浓香型白酒原酒的酒精度，具有较好的应用潜力，可为白酒原酒酒精度分析提供新的快速无损检测手段。摘 要：基于近红外光谱（NIR）及定量建模技术，建立一种快速无损的浓香型白酒原酒酒精度预测方法。通过采集129个浓香型白酒原酒样品的红外光谱数据，对比6种光谱预处理方法（均值中心化、卷积平滑、一阶导数、二阶导数、标准正态变换、多元散射校正），并分别采用多元线性回归（MLR）、主成分回归（PCR）、偏最小二乘回归（PLSR）、支持向量机回归（SVR）、反向传播人工神经网络（BP-ANN）5种建模方法构建酒精度预测模型。结果表明，标准正态变换结合MLR模型，训练集的决定系数为0.983 1，验证集的决定系数为0.967 3，残差预测偏差（RPD）为5.602 1，表现出较好的预测能力；此外，一阶导数结合SVR模型也显示出较高的预测精度，训练集的决定系数为0.971 2，验证集的决定系数为0.980 5，残差预测偏差（RPD）为7.257 3。综上，基于近红外光谱与机器学习结合的方法能够有效预测浓香型白酒原酒的酒精度，具有较好的应用潜力，可为白酒原酒酒精度分析提供新的快速无损检测手段。
中国白酒作为世界六大蒸馏酒之一，在世界范围内占据重要地位[1]。根据不同酿造工艺分为了主要的12种香型，其中浓香型白酒分布最为广泛，浓香型白酒的市场份额曾一度达到70%以上[2]。浓香型白酒以高粱为主要酿酒原料，辅以玉米、豌豆、糯米、小麦等，采用中高温大曲，泥窖固态发酵，采用续糟配料，混蒸混烧出酒。白酒中乙醇和水占据主要成分，占总量的98%以上，其他香味物质占白酒总量的1%～2%。因此白酒质量的好坏与酒精度密不可分，准确测定白酒中的乙醇含量能够有效的控制白酒质量安全。但传统检测手段如需准确无误的检测酒精度首先需要通过蒸馏法，再利用酒精计测量，这会破坏样品，且费时费力，无法实现快速无损检测。
近红外光（Near Infrared，NIR）介于紫外-可见光（visible ultraviolet，VIS）和中红外光（mid infrared radiation，MIR）之间，波长范围在780～2 526 nm之间，波数范围约12 500～4 000 cm-1[3]。近红外与中红外类似，谱区信息量丰富，几乎包含全部基团的信息；也与可见光谱类似，穿透物质的能力相对较强，可以进行复杂样品的无损检测。因此，近红外光谱被广泛应用在食品、医学、环境等领域物质的分析[4]。余松柏等[5]总结了红外光谱技术在白酒行业的应用，印证了近红外技术结合大数据能极大提高检测效率，实现快速分析，是未来可持续开展的研究项目。韩四海等[6]通过近红外技术结合偏最小二乘（partial least squares，PLS）法构建了基酒中乙醇的定量模型，所建模型具有很好的预测效果。王凡等[7]将气相色谱与近红外技术融合，利用偏最小二乘法建立了酱香型白酒6种醇类物质的分析模型，模型的预测准确度、稳定性良好。
本研究是基于近红外光谱及定量建模技术，建立一种快速无损的浓香型白酒原酒酒精度预测方法。收集浓香型原酒酒精度红外光谱数据，通过不同的光谱前处理手段（均值中心化、卷积平滑、一阶导数、二阶导数、标准正态变换、多元散射校正），进一步结合化学计量学和机器学习，应用多元线性回归（multiple linear regression，MLR）、主成分回归（principal component regression，PCR）、偏最小二乘回归（partial least squares regression，PLSR）、支持向量机回归（support vector regression，SVR）、反向传播-人工神经网络（backpropagation-artificial neural networks，BP-ANN）等算法构建定量分析模型。旨在融合近红外技术结合机器学习方法，构建一种快速、无损分析浓香型原酒酒精度的方法，突破传统破坏性检测方法的局限性，为原酒检测提供一种高效、实时的质量监控工具，具有重要的理论参考与实践价值。
浓香型原酒样品：取自四川浓香型白酒原酒某生产酒厂，共计129个样品。
QuasIRTM1000傅里叶变换近红外光谱（Fourier transform near infrared spectroscopy，FT-NIR）仪：四川威斯派克科技有限公司。
1.3.1 浓香型白酒原酒酒精度检测
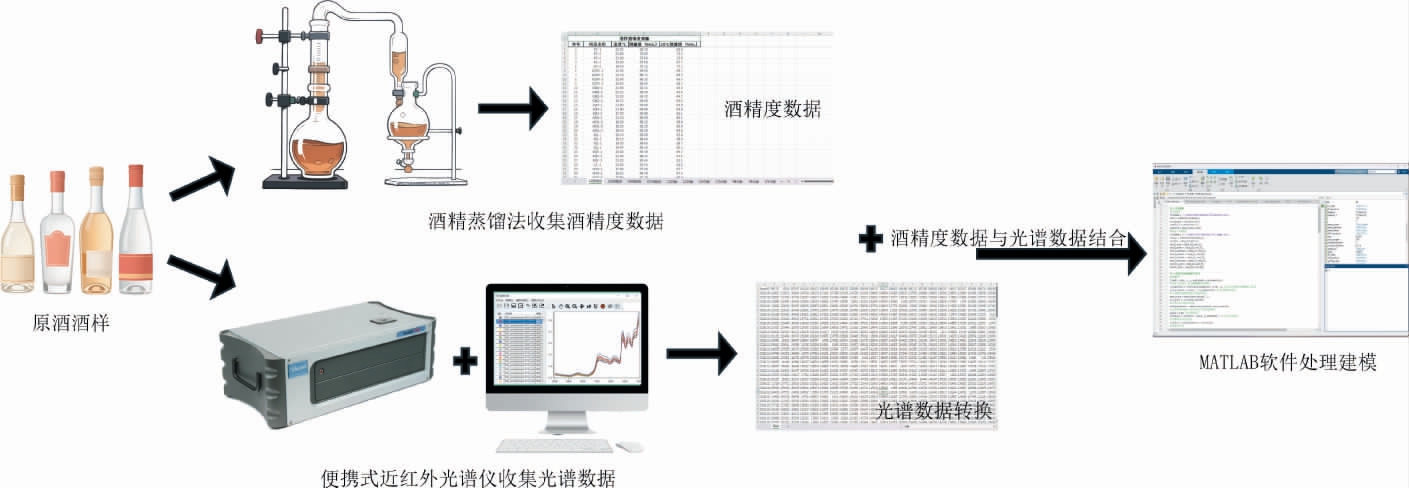
图1 浓香型白酒原酒酒精度检测示意图
Fig.1 Schematic diagram of alcohol content determination for original liquor of strong-flavor Baijiu
1.3.2 酒精计法测定浓香型白酒酒精度
浓香型白酒酒精度测定：参考国家标准GB 5009.225—2023《酒和食用酒精中乙醇浓度的测定》中的酒精计法[8]。
通过蒸馏去除样品中不挥发性物质，用酒精计测得酒精体积分数示值，通过査询酒精计温度与20 ℃酒精度换算表进行温度校正，求得样品在20 ℃时的酒精度。
1.3.3 近红外光谱测定酒精度
（1）近红外光谱数据采集
光谱扫描范围[9]：12 000～4 000 cm-1；分辨率8 cm-1；光谱扫描次数64次；重复次数1次；采集方式为液体透射。每个样品采集2次，取2次采集的光谱平均值作为样本的原始光谱数据，且在测量过程中，温度、湿度等环境条件尽量保持一致。
参比光谱：使用同一1 mm比色皿，采集空气和比色皿作参比光谱。采集光谱反映空气、白酒（水、乙醇、微量成分）和比色皿，扣除空气和比色皿的吸光度值，即样品光谱：白酒（水、乙醇、微量成分）的总吸收。
（2）数据处理
Excel2019对样本数据整合收集，利用MATLABR2024b对近红外光谱数据进行预处理，结合样本数据进行特征波长筛选，模型建立，模型评估。
异常样本剔除：马氏距离（Mahalanobis distance）法。
数据预处理方法：均值中心化（Mean centering），Savitzky-Golay（SG）卷积平滑，直接差分法（Norris）中：一阶求导、二阶求导，标准正态变换（standard normal transformation，SNV），多元散射校正（multiplicative scatter correction，MSC）。
特征波长变量筛选方法：基于PLS算法，将全光谱建立回归模型，根据回归系数，选择显著波长段，采用显著波长段应用于不同方式建模。
模型建立：多元线性回归（MLR）、偏最小二乘回归法（PLSR）、主成分回归（PCR）、支持向量机回归（SVR）、反向传播人工神经网络（BP-ANN）。
模型评估指标：决定系数（R2）是[10]评估回归模型性能的常用指标，它表示模型的预测值与实际值之间的拟合程度，反映了模型可以解释的目标变量总变异的比例；均方根误差（root mean square error，RMSE）是一种常用的回归模型性能评价指标[11]，用于量化预测值与实际值之间的差异；残差预测偏差（residual prediction deviation，RPD）是衡量回归模型预测性能的一个指标，通过比较模型预测结果与实际测量值之间的偏差来评估模型的预测能力[12]。其中决定系数R2越接近于1，表明模型预测准确性越高；RMSE越接近于0，表明模型预测稳定越高；RPD值在1.5～2.0之间表明模型预测能力较差，在2.0～2.5之间表明模型预测能力一般，可进行粗略的定量预测，在2.5～3.0之间或＞3，分别表明模型具有较好、优异的预测性能[10]。
采用酒精计法对129个浓香型白酒样品进行酒精度检测，结果表明，酒精度范围为51.4%vol～73.6%vol，平均值为65.00%vol，标准偏差为4.40%vol。
异常样本剔除可大致分为建立定量分析模型前和模型后2种。前者主要通过马氏距离等方法在大样本中进行异常剔除，后者是在训练集建立模型后通过残差分析等方法直接反映模型预测偏差，诊断模型缺陷，剔除异常样本，再次建立模型达到优化模型效果。本次主要是建立模型前进行异常样本剔除，马氏距离是一种衡量两个样本之间差异性的度量方法，它考虑了变量之间的协方差结构，能够有效地识别出与整体数据分布不一致的异常样本[13]，从而消除量纲影响。马氏距离法剔除异常样本结果见图2。由图2可知，通过马氏距离法结合卡方分布，自由度为1、显著性水平为0.01时，异常阈值线参数为6.634 9，剔除2个异常样本，用于建模分析样本总数为127个。
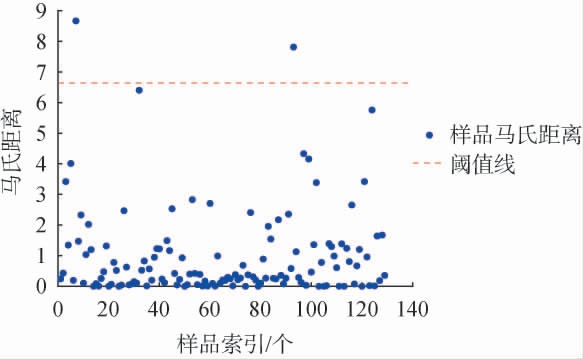
图2 马氏距离法剔除异常样本
Fig.2 Remove the abnormal samples by Mahalanobis distance method
2.3.1 训练集及数据集划分
标准偏差可以用来衡量数据分散程度的一个重要指标，其大小反映了数据点与整体均值之间的平均偏离程度[12]。采用Kennard-Stone（KS）算法[14]将样本集按7∶3划分为训练集和验证集，最终选择训练集样本89个，验证集样本38个，结果见表1。变异系数（coefficient of variation，CV）=（标准偏差/均值）×100%。由表1可知，两个数据集标准偏差接近，CV值均为6%左右，可以说明本次用于建模训练集和验证集离散程度均合适，数据集中稳定，用于建模有代表性。
表1 基于Kennard-Stone算法划分数据集
Table 1 Dataset partitioning based on the Kennard-Stone algorithm
项目 样本数 最大值 最小值 平均值 标准偏差训练集验证集89 38 73.6 72.4 53.6 54.3 65.299 64.976 3.996 4.414
浓香型白酒原酒酒精度近红外光谱分析原始数据结果见图3。
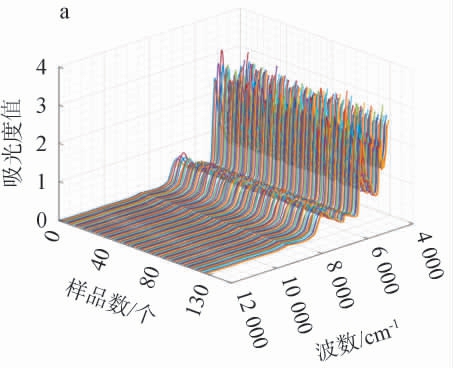
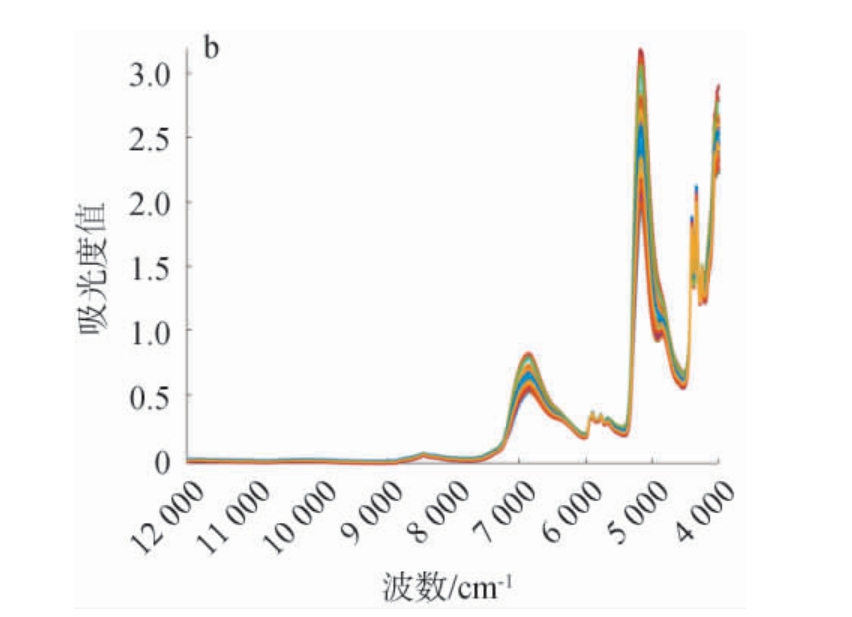
图3 浓香型白酒原酒样品酒精度近红外光谱分析原始数据
Fig.3 Raw data of alcohol contents of original liquor in strong-flavor Baijiu samples analysis by near-infrared spectroscopy
（a）瀑布图；（b）平面图。
由图3a可知，酒样在波数为12 000～4 000 cm-1范围的光谱图中出现明显的吸收峰。由图3b可知，不同颜色曲线的吸光度值高度、峰形存在细微差异，体现酒样因原料、工艺等导致的成分区别，进而导致酒精度的差异，说明光谱可区分样品间的酒精度潜在关联差异。
2.3.2 原始光谱原始数据预处理
光谱数据采集过程中受环境、仪器和操作的影响容易造成光谱存在基线漂移、液体导致光谱采集过程中出现了明显的散射现象等降低变量解释能力的干扰信息，相关研究表明[15-17]，需要通过不同的预处理方式，削弱或者消除光谱采集过程中因环境或仪器等因素的误差影响，从而提高数据信噪比，增强光谱数据的表征能力。本次研究主要选择均值中心化、卷积平滑、一阶导数、二阶导数、标准正态变换、多元散射校正等方法分别进行近红外光谱原始数据预处理，并将处理后的数据用不同的建模方法建模，对比分析最优预处理方法。各种预处理方法所得光谱对比分析，结果见图4。
图4 浓香型白酒原酒样品酒精度近红外光谱原始数据不同预处理方法
Fig.4 Different pretreatment methods of raw data of alcohol content of original liquor in strong-flavor Baijiu samples analysis by near-infrared spectroscopy
（a）均值中心化；（b）卷积平滑；（c）一阶导数；（d）二阶导数；（e）标准正态变换；（f）多元散射校正。
由图4a可知，均值中心化消除了光谱整体偏移，图中可见光谱以0为中心上下分布，不同样品间的光谱差异更聚焦于相对变化。由图4b可知，对比原始光谱图，出现基线漂移或波动，尤其是波数7 000 cm-1、5 000 cm-1附近，这可能由仪器噪声、样品散射或背景干扰引起，导致整体曲线不平稳。通过平滑等方法，噪声被有效降低，曲线变得平滑[18]。由图4c可知，计算光谱导数，增强了峰的边缘差异，图中吸光度值在峰的上升或下降沿出现正负峰（如波数4000～6000cm-1附近）。由图4d可知，二阶导数进一步计算变化率，强化了峰的精细结构，还可以分辨重叠峰，进一步提高分辨率[19]。由图4e可知，SNV对每个样品光谱做标准化，消除了样品间的光程差异和整体吸光度值的波动。由图4f可知，MSC主要是针对光谱中散射引起的基线漂移，能够很好校正样品间的光谱散射差异，与SNV方法都能使得不同样品之间的光谱更具可比性，并使吸收特征更加突出[20]。
采用偏最小二乘法（PLS）选择波段[21]，将全光谱等分为一定数量的子区间，采用子区间分别建立PLS模型，从PLS模型中获取回归系数，用于评价各波长的重要性，同时基于回归系数的标准差和分数位自动确定一个合理的阈值，选择绝对值大于阈值的波长并将连续的波长合并为波段[22]，最后确定的阈值为161.502。偏最小二乘法特征波段的筛选结果见图5。由图5可知，共筛选出3大波段4 416.3～4 106.7 cm-1，5 230.2～4 948.7 cm-1，11 814.1～11 123.6 cm-1，训练集和验证集用特征波段索引，用于后续定量模型建立。
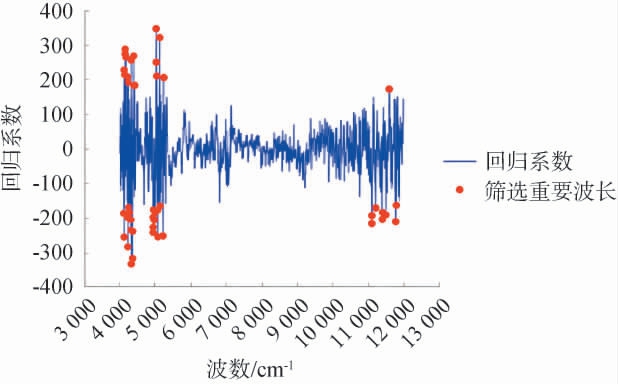
图5 偏最小二乘法特征波段的筛选结果
Fig.5 Screening results of the characteristic bands with partial least squares method
分析模型的建立通常包括两个阶段[23]：首先是训练阶段，研究量测方法，尝试建立数学模型，即建立两组变量之间的关系，Y=f（X）；第二阶段是预测阶段，对自变量使用回归系数来预测数值。而不同的量测方法，所建立的数学校正模型有一定的差异，不同方法从不同角度考虑自变量和因变量是否存在线性关系。用于近红外光谱数据定量分析的方法也主要分为线性回归方法[24]：多元线性回归（MLR）、偏最小二乘回归法（PLSR）、主成分回归（PCR）；非线性回归方法[25]：支持向量机回归（SVR）、反向传播人工神经网络（BP-ANN）。两种非线性方法与线性方法筛选结合的核心原则是：线性筛选用于降维与捕捉主要趋势，非线性模型用于拟合细节偏差，两者结合的有效性需通过数据分布和交叉验证验证。
本研究也将对比这5种模型建立方法及不同预处理方法所建立模型的差异，并找出最适建立浓香型原酒酒精度定量预测模型。各个模型涉及参数优化设置均通过网格搜索及5折交叉验证筛选最优参数，各个模型参数范围见表2。
表2 各个模型参数范围
Table 2 Parameter ranges of various models
模型 参数 参数范围PLSR PCR SVR BP-ANN主成分数主成分数惩罚因子ε-不敏感损失宽度隐层神经元数最大训练轮数1～30 1～20 0.00 1～1 000，10倍0.00 1～1，0.05 5～50，5 1 000～2 000，500
2.5.1 各模型精度评价指标
采用的各模型精度评价参数分别为训练集均方根误差（root mean-square error of train，RMSET）、训练集决定系数（determination coefficient of train，
）、验证集均方根误差（root-mean-square error of validation，RMSEV）、验证集决定系数（determination coefficient of validation，
）以及残差预测偏差（RPD），具体计算公式如式（1）～（5）所示。
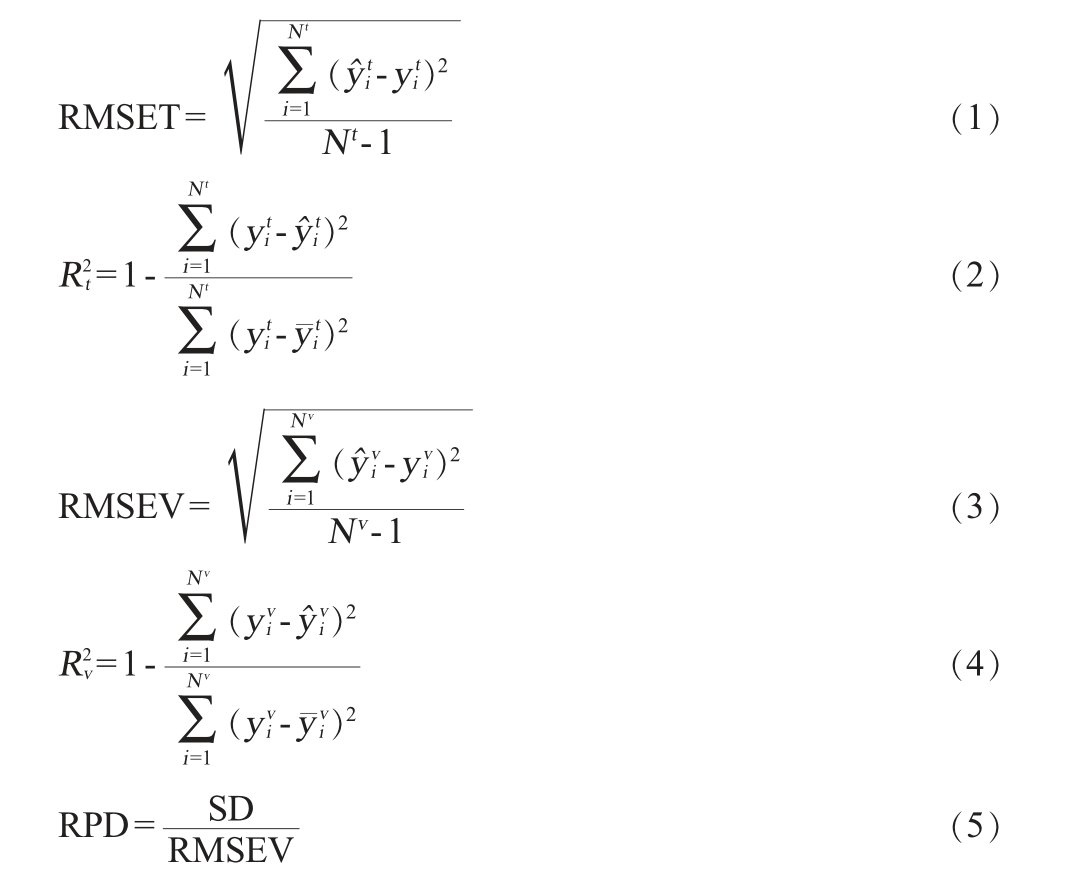
式中：Nt为训练集样本数，个；
和
分别为训练集第i个样品的实际值和预测值，%vol；
是训练集的平均值，%vol；Nv为预测集样本数，个；
和
分别为验证集的第i个样品的实际值和预测值，%vol；
是验证集的平均值，%vol；SD是验证集样本的标准差，%vol。
不同预处理及建模方法对各模型精度影响结果见表3，各模型评价指标对比结果见图6。
表3 不同预处理及建模方法各模型精度评价
Table 3 Accuracy evaluation of various models with different preprocessing and modeling methods
不同建模方法 预处理训练集验证集R2t RMSET R2 v RMSEV RPD MLR PLSR PCR SVR BP-ANN无处理均值中心化卷积平滑一阶导数二阶导数标准正态变换多元散射校正无处理均值中心化卷积平滑一阶导数二阶导数标准正态变换多元散射校正无处理均值中心化卷积平滑一阶导数二阶导数标准正态变换多元散射校正无处理均值中心化卷积平滑一阶导数二阶导数标准正态变换多元散射校正无处理均值中心化卷积平滑一阶导数二阶导数标准正态变换多元散射校正0.981 4 0.981 4 0.981 4 0.980 7 0.976 4 0.983 1 0.976 2 0.957 9 0.957 9 0.958 3 0.956 1 0.950 1 0.957 9 0.958 3 0.955 0 0.955 0 0.956 8 0.952 9 0.947 0 0.942 2 0.956 8 0.960 4 0.961 4 0.961 3 0.971 2 0.968 4 0.963 2 0.961 4 0.968 2 0.965 6 0.266 5 0.958 2 0.946 4 0.971 8 0.954 3 0.541 7 0.541 7 0.541 7 0.551 9 0.610 8 0.515 9 0.613 5 0.815 7 0.815 7 0.811 4 0.832 8 0.887 3 0.815 4 0.811 4 0.842 7 0.842 7 0.826 0 0.862 3 0.915 1 0.955 0 0.826 0 0.790 9 0.780 9 0.781 4 0.674 1 0.706 2 0.762 2 0.780 6 0.708 3 0.736 6 3.403 0 0.812 1 0.919 5 0.667 7 0.849 7 0.959 6 0.954 4 0.959 6 0.956 5 0.956 3 0.967 3 0.953 1 0.984 7 0.979 4 0.985 0 0.984 1 0.981 1 0.981 7 0.985 0 0.985 1 0.979 6 0.985 1 0.983 2 0.980 3 0.969 6 0.985 1 0.987 6 0.980 8 0.986 2 0.980 5 0.973 3 0.982 7 0.978 3 0.976 0 0.983 1 0.483 1 0.969 5 0.955 8 0.977 1 0.969 2 0.874 9 0.919 4 0.874 9 0.908 2 0.910 3 0.787 9 0.943 5 0.538 1 0.625 0 0.534 0 0.548 9 0.598 5 0.589 4 0.534 0 0.531 7 0.621 8 0.531 8 0.564 3 0.611 7 0.759 8 0.531 8 0.485 9 0.603 6 0.511 7 0.608 2 0.711 7 0.573 4 0.642 2 0.675 1 0.565 7 3.131 3 0.761 3 0.915 7 0.659 3 0.764 7 5.019 2 4.800 8 5.019 2 4.860 0 4.848 8 5.602 1 4.678 2 8.202 8 7.062 2 8.265 7 8.041 3 7.375 0 7.488 8 8.265 7 8.301 5 7.098 6 8.300 0 7.821 9 7.215 8 5.809 2 8.300 0 9.084 0 7.312 6 8.626 0 7.257 3 6.201 9 7.697 8 6.873 1 6.538 1 7.802 5 1.409 6 5.797 8 4.820 2 6.694 8 5.772 0
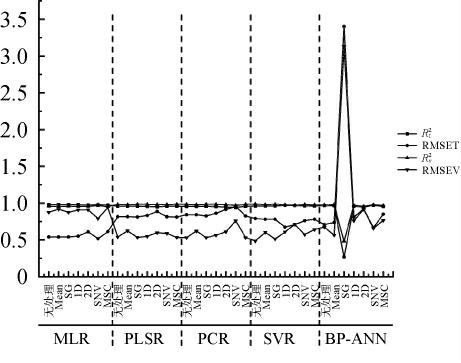
图6 不同预处理和建模方法各模型评价指标对比
Fig.6 Comparison of evaluation indexes of various models with different preprocessing and modeling methods
由表3可知，多元线性回归（MLR）用标准正态变换处理的训练集
最高（0.983 1），但验证集
较低，RPD为5.602 1，预测能力优秀。偏最小二乘回归（PLSR）和主成分回归（PCR）验证集的性能显著优于MLR，其中用卷积平滑处理的PLSR的验证集
最高（0.985 0），RMSEV 低至0.534 0，PCR表现类似，两种方法对预处理鲁棒性强，尤其卷积平滑效果稳定。支持向量回归（SVR）在无预处理时，验证集性能为所有方法中最优，
=0.987 6，RMSEV=0.485 9，RPD=9.084 0。反向传播人工神经网络（BP-ANN）模型表现整体波动较大，卷积平滑时，模型完全失效，验证集
为0.483 1，RPD为1.409 6。经过对比，如需挑选出最适合的模型，还要综合考量训练集
、RMSET，验证集
、RMSEV、RPD整体，因此结合图6对比不同预处理和模型方法，找出最适合预测原酒酒精度模型。
决定系数R2越接近1模型对数据的解释能力越强，RMSE越小预测误差越小，模型精准度越高，将训练集和验证集的评估参数综合考虑。不同处理和建模方法各模型评价指标对比结果见图6。由图6可知，MLR模型简单易解释，整体模型性能较优，经过SNV对光谱的干扰有效压制，线性算法MLR能够捕捉更多酒精度与光谱的线性关系。同时为了追求预测精度，选用SVR模型结合一阶导数，在验证集上有更低的RMSE，方法组合能探索酒精度与光谱更深的非线性关联。
对酒精度预测最终选用两种组合模型，一种是标准正态变换（SNV）结合多元线性回归（MLR），另一种是一阶导数结合支持向量机回归（SVR），预测效果结果见图7。
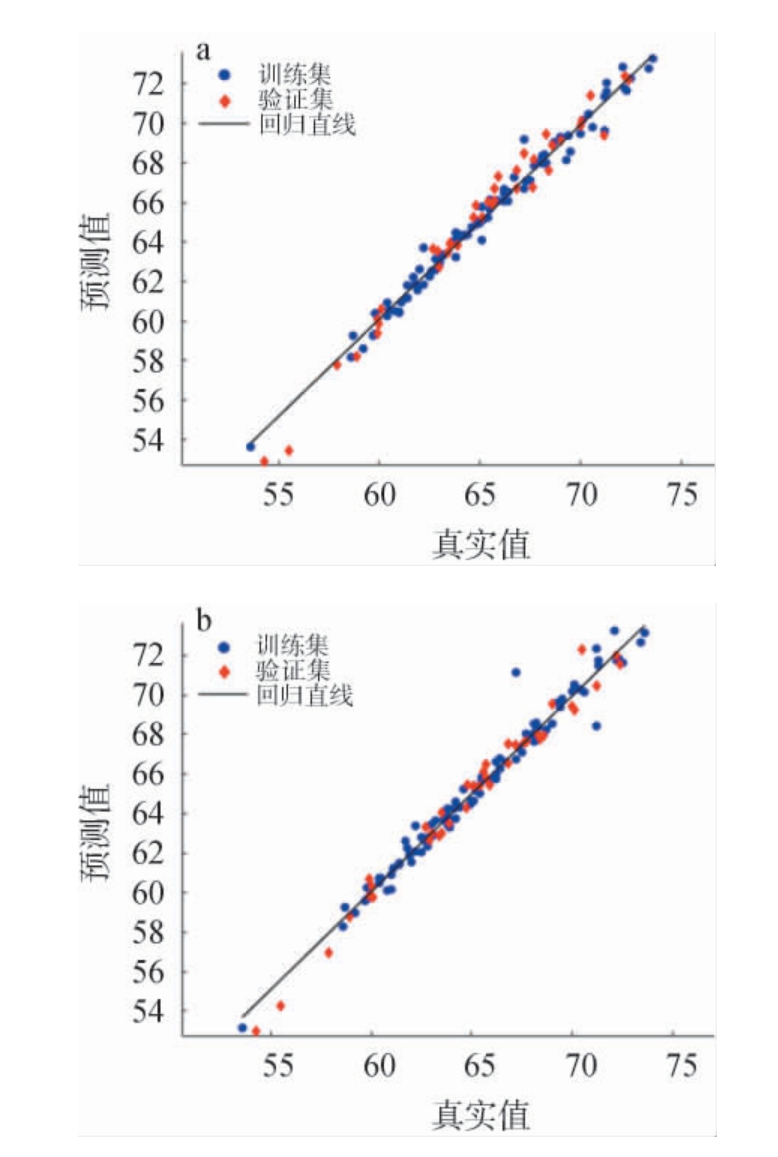
图7 两种回归模型对浓香型白酒原酒样品酒精度的预测效果
Fig.7 Predictive effect of the two regression models on the alcohol contents of strong-flavor Baijiu base liquor samples
（a）标准正态变换+多元线性回归（MLR）；（b）一阶导数+支持向量机回归（SVR）。
由图7可知，SNV和MLR组合，训练集的决定系数
为0.983 1，RMSET为0.515 9，
为0.967 3，RMSEV为0.787 9，RPD为5.602 1，回归方程为：y=0.983 1x+1.100 9；以及一阶导数结合SVR，
为0.971 2，RMSET为0.647 1，
为0.980 5，RMSEV为0.608 2，RPD为7.257 3，回归方程为：y=0.991 3x+0.569 1。结果表明，标准正态变换（SNV）+多元线性回归（MLR）模型真实值和预测值更好的分布在回归线上，模型表现更稳定、普适性更强。而一阶导数+支持向量机回归（SVR）明显有个别值偏离回归线，但展现了捕捉非线性关联的潜力。这样对比验证了预处理与算法适配性对模型效果的关键影响，为白酒结合光谱酒精度定量分析的方法选择提供了理论基础。
基于近红外光谱（NIR）结合定量建模技术，本研究成功构建了一种快速无损的浓香型白酒原酒酒精度预测方法。结果表明，通过PLS筛选3大波段（4 416.3～4 106.7 cm-1，5 230.2～4 948.7 cm-1，11 814.1～11 123.6 cm-1）重要特征波长，标准正态变换（SNV）结合多元线性回归（MLR）模型（训练集
，验证集
，RPD=5.602 1）与一阶导数预处理结合支持向量机回归（SVR）模型（训练集
=0.971 2，验证集
，RPD=7.257 3）预测性能最优，证实NIR技术结合机器学习能替代传统破坏性检测方法。未来的研究可以进一步探索更深层次的特征选择算法和深度学习模型，如目前已有应用卷积神经网络对酒醅酸度分析[26]。浓香型白酒质量方面还需要进一步提高预测精度，并扩展到其他关键质量指标的测定如总酸、总酯、己酸乙酯和己酸等[27]，为白酒原酒快速检测分析提供更加精准、高效的工具。
[1]廖丽，文静，邹永芳，等.中红外光谱快检技术在浓香型原酒风味分析中的应用研究[J].酿酒科技，2024（4）：36-45.
[2]胡景辉，陈禹锜，薛新新，等.浓香型白酒发展概述[J].中国酿造，2022，41（6）：24-30.
[3]LIU L,JIANG H,CHEN Q,et al.Rapid determination of acidity index of peanut during storage by a portable near-infrared spectroscopy system[J].Infrared Phys Techn,2022,127:104472.
[4]严衍禄，赵龙莲，韩东海，等.近红外光谱分析基础与应用[M].北京：中国轻工业出版社，2005：1-5.
[5]余松柏，黄张君，赵兴蓉，等.红外光谱技术及其在白酒酿造过程中快速检测与分析的研究进展[J].分析测试学报，2025，44（3）：544-561.
[6]韩四海，郭玉姗，李璇，等.基于近红外光谱技术检测白酒基酒中乙醇含量的研究[J].中国酿造，2018，37（9）：158-161.
[7]王凡，张文娟，李国辉，等.近红外光谱技术同时快速定量酱香型白酒基酒醇类物质[J].食品与发酵工业，2025，51（16）：324-331.
[8]国家卫生健康委员会，国家市场监督管理总局.GB 5009.225—2023食品安全国家标准酒和食用酒精中乙醇浓度的测定[S].北京：中国标准出版社，2023.
[9]李征，王媚，黄河，等.近红外光谱结合气相色谱对浓香型白酒基酒定性鉴别分析[J].中国酿造，2023，42（3）：222-228.
[10]JIANG H,LIU L,CHEN Q,et al.Rapid determination of acidity index of peanuts by near-infrared spectroscopy technology:Comparing the performance of different near-infrared spectral models[J].Infrared Phys Techn,2022,125:104308.
[11]ANJOS O, CALDEIRA I, FERNANDES T A, et al.PLS-R calibration models for wine spirit volatile phenols prediction by near-infrared spectroscopy[J].Sensors,2021,22(1):286.
[12]李蓉，郝璐，袁洪福，等.一种近红外光谱定量分析软件预测性能评价方法[J].光谱学与光谱分析，2025，45（1）：213-221.
[13]王加龙，马坤，高鹏，等.基于可见-近红外光谱技术研发便携式贝贝南瓜品质无损检测仪[J].食品科学，2025，46（6）：254-262.
[14]SHI Y,LV S,SHI K.A new parallel data geometry analysis algorithm to select training data for support vector machine[J].AIMS Math, 2021,6(12):13931-13953.
[15]王启，马辉峰，蔡建波，等.近红外光谱技术在北方浓香型白酒酿造糟醅理化指标快速检测中的应用[J].中国酿造，2023，42（12）：161-164.
[16]LIU J,SUN S,TAN Z,et al.Nondestructive detection of sunset yellow in cream based on near-infrared spectroscopy and interval random forest[J].Spectrochim Acta A,2020,242:118718.
[17]何思颖，孙安，赵蒙.近红外光谱在白酒检测中的研究进展[J].酿酒科技，2024（5）：111-117.
[18]JIAO Y,LI Z,CHEN X, et al.Preprocessing methods for near-infrared spectrum calibration[J].J Chemometr,2020,34(10):e3306.
[19]宗绪岩，李骥，邹永芳，等.基于化学计量学的近红外光谱法检测白酒中酯含量研究[J].农产品加工，2019（4）：53-55，59.
[20]SCHOOT M,KAPPER C,VAN KOLLENBURG G H,et al.Investigating the need for preprocessing of near-infrared spectroscopic data as a function of sample size[J].Chemometr Intell Lab,2020,204:104105.
[21]SILALAHI D D,MIDI H,ARASAN J,et al.Robust generalized multiplicative scatter correction algorithm on pretreatment of near infrared spectral data[J].Vibrat Spectrosc,2018,97:55-65.
[22]HONG S,WANG Y,CHEN A,et al.Rapid assessment of gasoline quality by near-infrared (NIR) deep learning model combined with fractional derivative pretreatment[J].Anal Lett,2022,55(11):1745-1756.
[23]杨国迪.基于近红外光谱的白酒基酒分析模型的建立[D].洛阳：河南科技大学，2016.
[24]陈霏，庹先国，曾祥林，等.近红外检测技术在白酒生产中的应用研究进展[J].食品科技，2021，46（1）：280-284.
[25]VIA B,MCDONALD T,FULTON J.Nonlinear multivariate modeling of strand density from near-infrared spectra[J].Wood Sci Technol, 2012,46(6):1073-1084.
[26]王琦标，何余锴，罗雨诗，等.基于卷积神经网络和近红外光谱的酒醅酸度分析方法研究[J].光谱学与光谱分析，2023，43（12）：3726-3731.
[27]狄大铃.快速检测技术在白酒质量检测中的应用[J].现代食品，2023，29（14）：76-78.
Analysis of alcohol content of original liquor of strong-flavor Baijiu based on near-infrared spectroscopy and quantitative modeling technology
Abstract：A rapid and non-destructive method for predicting the alcohol content of original liquor of strong-flavor(Nongxiangxing)Baijiu was developed using near-infrared(NIR)spectroscopy combined with quantitative modeling techniques.Infrared spectral data of 129 original liquor samples of strong-flavor Baijiu were collected,and 6 spectral pretreatment methods(mean centralization,convolution smoothing,first derivative,second derivative,standard normal transformation,and multivariate scattering correction)were compared.The alcohol content prediction models were constructed by using 5 modeling methods:multiple linear regression(MLR),principal component regression(PCR),partial least squares regression(PLSR),support vector machine regression(SVR), and backpropagation artificial neural network (BP-ANN).The results showed that when the standard normal transform was combined with the MLR model,the coefficient of determination
of the training set was 0.983 1,the coefficient of determination
of the validation set was 0.967 3,and the residual prediction deviation(RPD)was 5.602 1,demonstrating a good predictive ability.In addition,the firstorder derivative combined with the SVR model also showed a relatively high prediction accuracy.The coefficient of determination
of the training set was 0.971 2,the coefficient of determination
of the validation set was 0.980 5,and the residual prediction deviation(RPD)was 7.257 3.In conclusion,the method based on the combination of near-infrared spectroscopy and machine learning could effectively predict the alcohol content of the original liquor of strong-flavor Baijiu,and had good application potential.It could provide a new rapid non-destructive detection means for the alcohol content analysis of the original liquor of Baijiu.